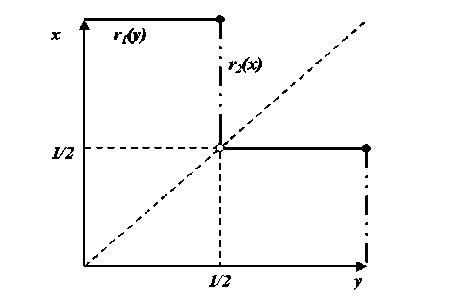
Figure 2: Reaction curves are constant except for a jump down, which precludes
symmetric equilibrium.
The number of equilibria may be obtained by finding the explicit form of
the reaction curves.
1 ify ≤ 1/2 1 ifx ≤ 1/2
r1 (y)= r2 (x)=
(13)
I 1/2 if y> 1/2 I 1/2 if x> 1/2
Figure 2 illustrates that there exists exactly one pair of pure strategy Nash
equilibria, namely (1, 2 ) and ( 2, 1) .
We can compare equilibria from the point of view of player 1, using the dual
to the Theorem 3.3. The payoff function of player 1 when x ≤ y, is constant
along his best reply, i.e. L2(r1 (y) ,y)=0. Therefore we conclude that player 1
prefers the equilibrium where he is more active.
4 Endogenous heterogeneity without monotonic
best replies
In the previous section we discussed symmetry breaking via strategic substitutes
and nonconcavity of the payoff function. In this section we extend the analy-
sis from the previous section to encompass other forms of strategic interaction.
18
More intriguing information
1. An Estimated DSGE Model of the Indian Economy.2. The Role of Immigration in Sustaining the Social Security System: A Political Economy Approach
3. A NEW PERSPECTIVE ON UNDERINVESTMENT IN AGRICULTURAL R&D
4. Social Irresponsibility in Management
5. Labour Market Institutions and the Personal Distribution of Income in the OECD
6. Delayed Manifestation of T ransurethral Syndrome as a Complication of T ransurethral Prostatic Resection
7. PRIORITIES IN THE CHANGING WORLD OF AGRICULTURE
8. Measuring Semantic Similarity by Latent Relational Analysis
9. Locke's theory of perception
10. The ultimate determinants of central bank independence