Reputations, Market Structure, and the Choice of Quality Assurance Systems in the Food Industry

choose the level of output that maximizes per-period profits in the standard way to find the

Nash equilibrium levels y ^* (s ,s_- ), = 1,2 . We now write the first-stage problem for firm as

max
s ∈S

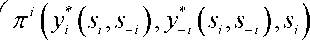
1-βm (s )m_- (s_- )

= max
s ∈S

' ^π ( s^{, s}-i∙) ^λ

₄¹^-^β^mi( si )^m -i(^s _i.)_y

which has the first-order condition

(6)

__________1__________(∂∏(si,s-i ) + ∏(s_ι,s-i)βm-_ι(s-i) ∂mi(si)
I^-βm₁( s_ι)^m- i ( s- i )^ ^dsi (1-^β^mi( si)^m- i ( s-.)) ^dsi ^

≤0s_i ≥0i=1,2

and the corresponding complementary slackness conditions. Note that if it is difficult to detect

quality deviations (i.e., when ω→0), the model predicts that processors will find it optimal

(** 7

s₁=0,s₂=0)).⁷ The

same result holds if β = 0 or when the probability that the processor’s rival is caught is close

to one.

The second-order sufficient conditions are

a1,1 a1,2 1

a2,1 a2,2 _ (1 - βm₁ m₂ )²

∂²E∏¹ ∂²E∏¹

∂s₁² ∂s₁∂s ₂

∂² E ∏² ∂² E ∏²

∂s₂∂s₁ ∂s₂²

ai,i ⁼

∂ ²πⁱ∂si

_∂2m

^{- βm}i^m-i) ⁺^π -y—

∂s_i²

βm_-_i ≤0

∂²πⁱ∂πⁱ∂mπⁱβ∂m∂m

and Ω =a_i_,_ia_-_i_,_-_i-a_i_,_-_ia_-_i_,_i>0 , for

a_{i i} =-----(1-βm_im _i ) +--ⁱ- βm _i +------—- —ⁱ--^l

, ''s⅛-i ⅛-i ^l^s (¹^-^βmi^m-i) ^l^s &_i

i=1,2.