Tariff Escalation and Invasive Species Risk

DI=D+I, the total use of raw input. The production function for the domestic final good is

DFG = DI^θK^λ-θ with θ ∈ (0,1).

Profit maximization leads to the derived input demand and supply of DFG as follows:
where P_DI is the input price and P_DFG is price of DFG.

DI^d

K ,

and DFG^s =

( P
_PD_

I ΘPdfg

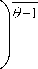
K,

Turning to demand, the demand for the processed good comes from the consumer of the
processed final products, FG. Domestic and imported processed goods, DFG and IFG, are
assumed perfect substitutes for the consumer. For simplicity’s sake we assume quasilinear
preferences for the processed goods. The utility of the consumer is a function of these two goods
and an aggregate all other goods, AOG. This is expressed as U(DFG+IFG, OAG) with

γ-1

U(FG, AOG) = AOG + —— FG ^γ where γ > 0, and FG = DFG + IFG.

γ-1

Utility maximization subject to a budget constraint, with AOG as numeraire, leads to the
demand for processed goods as FG = P_fg^-γ or the inverse demand P_fg = FG~^ιzγ.

Suppose imported input I is subject to an ad-valorem tariff t_I , that is, P_I=WP_I(1 +t_I) ,
and imported processed good IFG is subject to an ad-valorem tariff t_IFG leading to

P_IFG = WP_IFG (1 +t_IFG). Suppose that, initially, tariff escalation is in place, i.e., t_I <t_IFG. By
normalizing world prices equal to 1 without any loss of generality and using tariff factors
denoted by τ we have P=τ =(1+t) and P=τ =(1+t) .

II      I       IFG IFG      IFG

3.2. IS associated with imported input

Suppose input D is produced with an increasing marginal cost. Suppose that the frequency of IS

<<   4   5   6   7   8   9   10   >>

More intriguing information