A dynamic approach to the tendency of industries to cluster

Given that the consumers in both regions have the same preferences, the (marshallian)
demands can be expressed as in Equation (2) and (3). Since all varieties enter the utility
function in a symmetric fashion, the subscript for variety ( i=1, .∏ ) is ignored.

(2)       z 11 = m 1 p-_t ° P ° ^-1,        Pf^-1 = ^¹- . *^{p t}>'

n₁        n₂

(3)       z 12 = m 2 (P1t )^- ° P°^-1,     P°-^{1   (p/l} + ^p'

n₁        n₂

z11 is the demand for a particular variety produced in region 1 and sold in region 1 and
z21 is the demand for a particular variety produced in region 2, but sold in region 1. P₁ and
P₂ are the price indexes in the respective regions. n1 is the total number of manufacturing
firms producing in region 1 and n2 is the total number of manufacturing firms producing
in region 2. ° >1 is the price elasticity of demand for an individual variety,
(∂ ln z/ ∂ ln p = ° ).

The profits of a firm located in region 1, π ₁, is given by,

⁽⁴⁾       ^ 1 = ⁽P1 ^- c1⁾⁽ zu ⁺ z 12 ^{)- c}1^f

where c1 is marginal cost and c1f is fixed costs. The condition for profit maximization,
i.e. p ₁ (1 - ° ^- )= c ₁, together with the zero profit condition implies that firm scale is

independent of costs.

^{(5)       z} 11 ^{+ z} 12 = ^{f (}° ^{- 1)}

In order to explore how the industry is located between the two regions the relative
production value, relative cost and relative expenditure is used.

l _≡ n2P2⁽z22 ⁺ z21) _{p ≡} c_ = P2    _{η ≡} m2

ⁿ1 P1^(z 11 ^{+ z}12) ^{,         c} 1    P1 ^{,          m}1

In Equation (6), l is the relative production value. p is the relative cost (and also
relative price⁶) and η is the relative expenditure. Expressing the ratio of the price indexes
in terms of p and l leads to Equation (7).

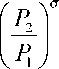
(7)

⁶ This follows from the fact that P1^{(1 -} ° ' ⁾= ^c1 under profit maximization, i.e. marginal revenue equals
marginal cost.

<<   3   4   5   6   7   8   9   >>

More intriguing information