Unilateral Actions the Case of International Environmental Problems

Result 1: A separating equilibrium exists, if there exists a q_i^' < q_i(H,0), such
' _ . . ..... . ' _ . . .....

thatNBi(H,q^'i,0)-NBi(H,q(L,1),1)>NBi(L,q^'i,0)-NBi(L,q(L,1),1)
Proof, see appendix 2.

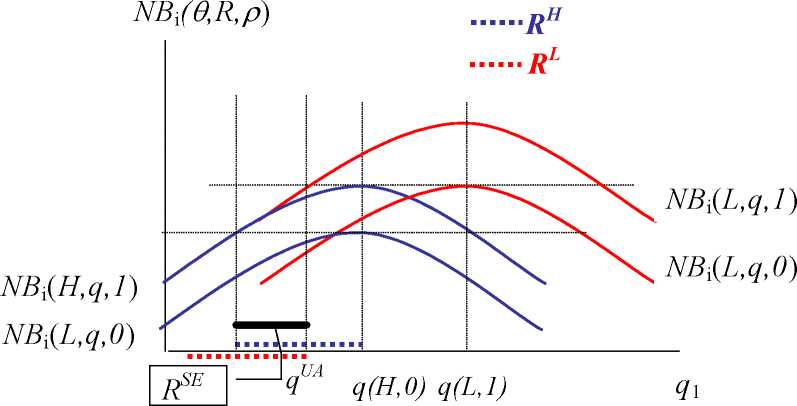
The necessary condition says that it must be less costly for the high cost type
than for the low cost type to decrease reductions below qi(H,0) defined by the
condition in result 1. In this way it resembles a sorting condition well-known
form the signalling literature. Figure 3 explains this condition. Typically, the set
of separating equilibrium outcomes is large, and this shortcoming will be dealt
with now by introducing equilibrium refinements.

Figure 3. The set of separating equilibrium outcomes

Equilibrium refinements used for signalling games are based on the notion of
forward induction, which asserts that when rational players enter a game, they
should, in evaluating strategies, reason from the beginning of the game-tree by
using introspection, i.e., by examining who has an incentive to send possible
out-of-equilibrium messages, and then revise beliefs accordingly. Given that it
is common knowledge among the players that everyone engages in this intro-
spection process, an implicit communication emerges. To see how refinements
based on this idea work, imagine that a player picks a candidate equilibrium

20

<<   15   16   17   18   19   20   21   >>

More intriguing information