Large-N and Large-T Properties of Panel Data Estimators and the Hausman Test

mixing model. For this model, we can establish the joint limits of the sample
averages of panel data whose time series are non-ergodic, as we show in Section
4 and Appendix.

Suppose that (Ω, F, P) is a basic probability space, and G, H, Z are sub-
sigma fields of F with Z ⊂ G and Z ⊂ H. Then, a conditional α-mixing coeffi-
cient between two sub-sigma fields G and H on Z is defined as

αz (G, H)= sup   ∣PZ (G ∩ H ) - Pz (G) Pz (H )∣,        (31)

G∈G, H∈H

where PZ (∙) denotes a conditional probability defined on the sigma field Z.¹0
This conditional α-mixing coefficient is a straightforward extension of the usual
α-mixing coefficient, except that it uses the conditional probability P_z (∙) in-
stead of the usual unconditional probability P (∙).

The general definition of the conditional α-mixing coefficient can apply to
our panel data model as follows. Suppressing the subscript i for convenience,
assume that {x_t }_t and z are scalar random variables, respectively defined in the
probability space (Ω, F, P), where sup_t E ∣x_t∣2^q < ∞, for some q > 1.¹¹ Define

F_-∞ = σ (..., x_t-1 ,x_t);F_t+d = σ (x_t+_m , x_t+_m+1 , ...);Z = σ(z),

where Z is assumed to be a non-trivial sigma field, i.e., in Z there exists a
subset A of Ω with 0 < P (A) < 1. Define

αz (d) = sup      sup      ∣PZ (G ∩ H) - Pz (G) Pz (H)∣.     (32)

t G∈F-^t∞,H∈F_t^∞_+d

With this definition, we will say that the sequence {xt} is conditionally α-mixing
if and only if

αz (d) → 0 a.s. ,                             (33)

as d →∞, where the almost sure convergence of α_z (d) holds with respect to
an outer probability measure P * of the probability space (Ω, F, P ).¹²

A technical problem in using the conditional α-mixing coefficient α_z (d) (as
well as αz (G,H)) is that it is not necessarily measurable with respect to the
conditioning sigma field Z . This problem raises some technical difficulties in
deriving useful inequalities. For example, following the usual techniques related
to (unconditional) α-mixing coefficients, one may expect that the following
conditional versions of α-mixing inequalities hold:

1

|EZ (xtxt+d)-(EZxt) (EZxt+d)∣ ≤ 2-q~⅛z (d)^—~´(≡up(Ez ∣xt∣^2q ´
q-1             t

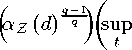
1

EZ ∣xt∣^2qj) q

¹⁰ We also could define similar conditional mixing coefficients of β- mixing and φ- mixing.

¹¹The xt need not be strictly stationary.

¹²For the details of the outer probability measure P *, readers may refer to Chapter 1.2 of
van der Vaart and Wellner (1996).

17

<<   14   15   16   17   18   19   20   >>

More intriguing information