Neural Network Modelling of Constrained Spatial Interaction Flows

telecommunication flow matrix (t_jj j, a (32, 32)-distance matrix (d_ij j, and gross
regional products for the 32 telecommunication regions - a set of 992 3-tupel
(s_j,d_ij,t_jj) with i, j = 1,...,32 (i ≠ j) was constructed. The first two components
represent the input variables x_2j_₁ and x_2j of the j-th module of the network model
¹CSL (x, w), and the last component the target output. The bias term b_i^ is clamped to
the scalar 1/ t_i.. s_j represents the potential draw of telecommunication in j and is
measured in terms of the gross regional product, d_ij in terms of distances from i to j,
while t_jj and t_i. represent telecommunication traffic flows. The input data were
preprocessed to data scaled into [0.1, 0.9]¹⁰.

The telecommunication data used stem from network measurements of carried traffic in
Austria in 1991, in terms of erlang, an internationally widely used measure of
telecommunication contact intensity, which is defined as the number of phone calls
(including facsimile transfers) multiplied by the average length of the call (transfer)
divided by the duration of measurement¹¹ [for more details, see Fischer and Gopal
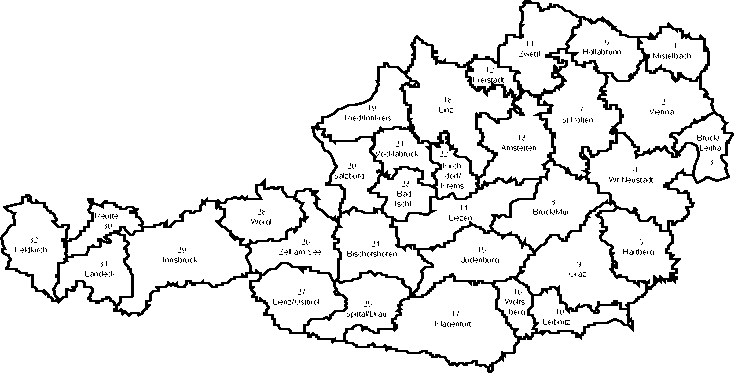
1994]. The data refer to the telecommunication traffic between the 32
telecommunication districts representing the second level of the hierarchical structure
of the Austrian telecommunication network (see Figure 2). Due to measurement
problems, intraregional traffic (i.e. i = j) is left out of consideration.

Hollabrunn

Mistelbach

Vienna

StPnlten

21

22

WrNeustad

Bruck/Mur

Wnrg

Hartberg

Judenburg

Spittal/Drau

Klagenfur

Bruck/

Leitha

23

Bad

sch

18

Linz

Kirch

dorf/

Krems

Reutte

30

20

alzburg

16

Wolfs

berg

14

Lieze

10

Leibnitz

31

Landeck

32

Feldkirch

29

nnsbruck

13

Amstetten

26

Zell am See

27

Lienz/Osttiro

19

Ried/Innkreis

24

Bischofshofen

Figure 2: The Regional System for Modelling Interregional Telecommunciation
Traffic in Austria

One of the simplest methods for estimating the prediction error is data splitting. This
method simulates model validation with new data by partitioning the total data set of

22

<<   21   22   23   24   25   26   27   >>

More intriguing information