(1984) for estimating NB models with panel data. This method has the advantage of
factoring out the overdispersion parameters and accounting for heterogeneity in the data.
To account for the fixed individual effects in the NB model, we rewrite the Poisson parameter
as,
⅛ = им (1)
where,
μit = E(nit) = exp(â Xit) i = 1, 2,....N t = 1, 2,........T (2)
in which μit is the Poisson parameter indicating expected numbers of casualties in an
observation unit i in a given time period t, nit is the number of observed casualties in an
observation unit i during a given time period t, Xit is a vector of covariates which describe
the characteristics of an observation unit i during a given time period t, â is a vector of
estimable coefficients representing the effects of the covariates, and (X. is the individual-
specific fixed effect. To derive the joint probability of the fixed effect NB model, it is
necessary to find a convenient distribution for the sum of events for a given individual,
∑nit . A detailed derivation can be found in Hausman et al. (1984). The resulting joint
probability of the ith individual conditional on total years is
Pr(ni1,
,niτ | ∑tnit) =
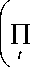
Γ( μit + nlt ) '^
Γ( μit )Γ( nit ) + 1 J
Γ(∑ t μit )Γ(∑ tnit + 1)
. Γ( ∑ t μit + ∑ tnit ) .
(3)
which includes â via μit but does not include ц and the overdispersion parameter k. From
this the likelihood function can be derived as,
L(Σtnit | nt,......,niτ) = ∏
t
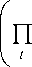
Γ( μit + nit ) jχ
Γ( μu )Γ(nit ) + 1 J"
∣rΓ(∑ t μit )Γ(∑ tnit + 1)ʌ
I Γ(∑tμit +∑tnit) J
(4)
11
More intriguing information
1. The name is absent2. Banking Supervision in Integrated Financial Markets: Implications for the EU
3. Foreign direct investment in the Indian telecommunications sector
4. PACKAGING: A KEY ELEMENT IN ADDED VALUE
5. Direct observations of the kinetics of migrating T-cells suggest active retention by endothelial cells with continual bidirectional migration
6. Tax systems and tax reforms in Europe: Rationale and open issue for more radical reforms
7. CONSUMER PERCEPTION ON ALTERNATIVE POULTRY
8. Social Balance Theory
9. The name is absent
10. Outsourcing, Complementary Innovations and Growth