The Role of area-yield crop insurance program face to the Mid-term Review of Common Agricultural Policy

The positive and negative components of the game are determined by the following
expressions, with -m ≤ i ≤ s

0s

V(y^-) = ∑ hi^- v(xi) and V(y⁺) = ∑ h_i⁺ v(x_i)
i = -m                        i = 0

(2) where:

h- decision weights;

v- value function; and,
x- results.

The value function has the following characteristics: (i) defined on deviations starting
from the reference point; (ii) concave for gains (v ' ' (x) < 0, for x>0) and convex for
losses (v ' ' (x)>0, for x < 0); (iii) steeper for losses than for gains. The graphic
representation is as follows:

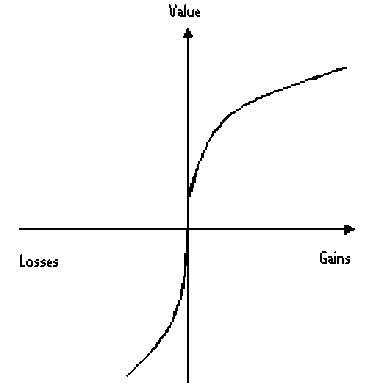
Figure 1 - The value function

<<   3   4   5   6   7   8   9   >>

More intriguing information