The Dictator and the Parties A Study on Policy Co-operation in Mineral Economies

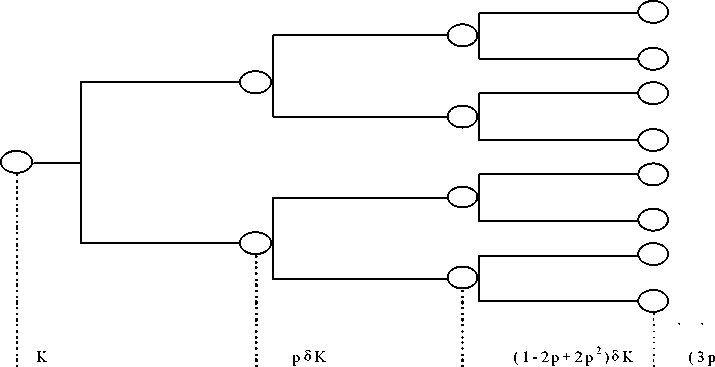
Figure 1: Probability tree of electoral gains

-6p² + 4p²) δ K

The development of the payoffs during electoral periods is:

1¹ = K[1 + pδ + (1 - 2p + 2p²)δ² + (3p - 6p² + 4p³)δ³ +

,     ...      ₁ „ .      ₁ δ•

+ (1 -4p +12p² - 16p³ + 8p⁴)δ⁴...(≡ 1)δ’^-1 + (≡ 2-)-—-]
^{2           2} (1 - δ )

At time t = 0 (current electoral period), Party I is the incumbent and enjoys K utils. During this
period she spends x0 and obtain a probability of being re-elected p. Thus, during the second
electoral period she will be in office (in) with probability p, or in the opposition (out) with
probability (1 - p). The expected discounted payoff for this second period is then equal to δ
[pK + (1 - p)0]. The analysis of the third period includes four possible cases, in two of them
Party I is in office with her payoff being equal to δ ² (1 - 2p + 2p²). For periods occurring far
into the future the probability of being in office converges to a half. Also, note that due to the
presence of discounting, expected gains get lower as times goes on.

Next the situation depicted by the probability tree will be presented in a more formal manner. In
general, at time t the total expected pay-off for the incumbent (Party I) is given by:

(1) It = p(x_t )δt+1 I}+1 + [1 - p(x_t )]δt+1 I0+1 + K

(2) I0+1 = [1 - q ( x∣+1 )] δt+2 I1+ 2 + q ( x⅛ ) δ_t+2 I0₊ 2

where: I_z¹ = 1¹( W_t ) ; Γ_m = 1¹( W_t+ r - x 1) ; ⅛2 = 1¹( W_t + 2 r - x 1 - x 2)

<<   8   9   10   11   12   13   14   >>

More intriguing information