|
Table B1 |
Kolmogorov-Smirnov tests on the distribution of the productivity index | |||
|
(A) |
(B) | |||
|
Obs |
KS statistic |
Hip |
KS statistic | |
|
__________(p-value)______ |
(p-value)________ | |||
|
IEa)=1 |
-0.0145 | |||
|
3O5 |
O.2515*** |
G(IE=O)>F(IE=1) |
(0.961)_________ | |
|
vs |
(O.OOO) |
0 2515*** | ||
|
IE=0 |
635 |
G(IE=O)<F(IE=1) |
. (0.000)_________ | |
|
SAMEb)=1 |
195 |
O.2946*** |
G(SAME=O)>F(SAME=1) |
-0.0235 (0.929)_________ |
|
SAME=0 |
72O |
(O.OOO) |
G(SAME=O)<F(SAME=1) |
0.2946*** (0.000)_________ |
|
NORTHc)=1 |
-0 0293 | |||
|
24O |
O.O959 |
G(NORD=O)>F(NORD=1) |
. (0.803)_________ | |
|
NORTH=0 |
675 |
(O.164) |
G(NORD=O)<F(NORD=1) |
0.0959 (0.196)_________ |
|
Notes : | ||||
a) Indicator variable that takes the value of 1 if the IE Index is greater than zero and the value zero otherwise
b) Indicator variable that takes the value of 1 if the IiEj (i=j) index is greater than zero and the value zero otherwise.
c) Indicator variable that takes the value of 1 if the IiEj (i=N &/or j=N) index is greater than zero and the value zero otherwise.
Figure B1. Cumulative conditional distributions (IE Index)
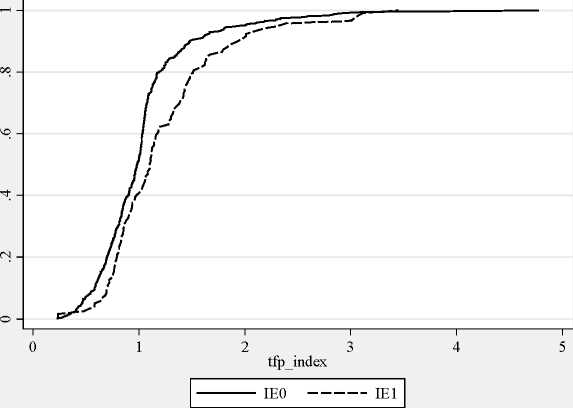
Figure B2. Cumulative conditional distributions (IE Index)
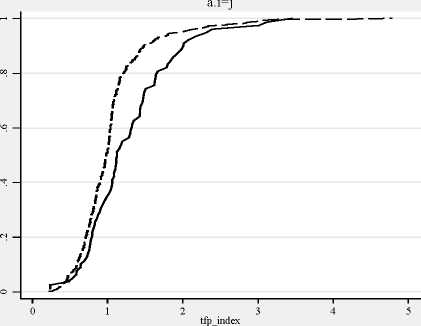
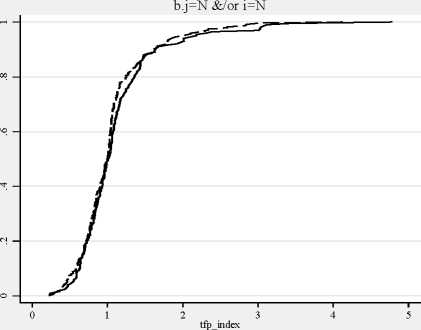
Same=I ----Same=O North=I ----North=O
4O
More intriguing information
1. Social Balance Theory2. AN ECONOMIC EVALUATION OF COTTON AND PEANUT RESEARCH IN SOUTHEASTERN UNITED STATES
3. Educational Inequalities Among School Leavers in Ireland 1979-1994
4. Party Groups and Policy Positions in the European Parliament
5. Mean Variance Optimization of Non-Linear Systems and Worst-case Analysis
6. The name is absent
7. News Not Noise: Socially Aware Information Filtering
8. The name is absent
9. Factores de alteração da composição da Despesa Pública: o caso norte-americano
10. Philosophical Perspectives on Trustworthiness and Open-mindedness as Professional Virtues for the Practice of Nursing: Implications for he Moral Education of Nurses