The Veblen-Gerschenkron Effect of FDI in Mezzogiorno and East Germany

in Markusen and Maskus (2001) in general equilibrium models comprising both
horizontal and vertical FDIs, when trade costs fall FDI between a given pair of
countries may either rise or fall depending on countries’ characteristics. In this
paper we propose a model that provides an alternative explanation based on
the incompleteness of outsourcing contracts.

3 The Model

Consider a country M endowed with L units of labour supplied inelastically by
L identical workers. Workers share the same preferences defined over a unit-
measure continuum of horizontally differentiated good Y and a homogenous
good Z:

U =ln

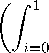
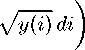
+ z.

where y (i) is the consumption of variety i of good Y and z is the consumption
of the homogenous good Z. Utility maximization then generates demands:

y(') = Ap(ⁱ)^-2,A = R⅛d-              (²)

_i=0 p(i) di

where A is a measure of the local “market potential”, which is increasing in the
size of the market (L) and in the price of competing varieties.

Good Z is produced under perfect competition using one unit of labour per
unit of output. This good is freely traded on international markets and it is
chosen as numeraire. Due to marginal cost pricing, this implies that also the
equilibrium wage equals unity. Good Y is produced under monopolistic com-
petition using a proportional amount of an intermediate good X per unit of
output. There is a one-to-one relation between varieties and firms. Intermedi-
ates are variety-specific and one unit of intermediate is produced by one unit of
labor.

In sector Y all firms are foreign-owned and supply the local market under
three alternative modes. Under the final export mode (henceforth, mode X),
intermediate and final productions take place abroad and the final output is
shipped to M . In this case the production of y(i) units of variety i requires an
equal amount of units of a variety-specific intermediate input x(i). Shipments
face iceberg trade costs: for each unit shipped only a fraction τ ∈ (0, 1) reaches
its final destination.

Under the intermediate export mode (henceforth, mode E), intermediates
are produced abroad and then shipped to country M where final production
takes place. For simplicity, we assume that intermediates incur the same trade
cost τ as the final products. In this case, the production of y(i) units of variety
i requires spending an amount I (i)² of the numeraire in market M where I(i)
represents the amount of investment (FDI) in assembly. Such investment is

<<   4   5   6   7   8   9   10   >>

More intriguing information