11
To achieve robust results, both tests described so far require large samples. How-
ever, Harvey et al. (1997) recommend a modified test statistic in small samples:
MDMjh =
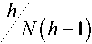

DMjh.
(3.8)
The critical values for this test are taken from the tN-1 distribution.
Forecast breakdown test
To evaluate the alternative inflation forecasts further, we also check the models
for a forecast breakdown (FB). This is defined as a situation in which the out-of-
sample forecasting performance of a forecast model is significantly worse than its
in-sample fit (Giacomini and Rossi 2006). To implement this check we compare
each model’s forecasting performance - measured by its mean squared forecast
error - to the expected forecast error based on its in-sample-fit.8 Analytically, a
“surprise loss” ( sl ) at time t is calculated as difference between the out-of-sample
loss and the average in-sample loss lt jh ,
sPj = (ej )2 - ljh
s t+h = (et+h ) - t .
(3.9)
If forecast model j is reliable, the mean of the associated surprise losses sl ,
taken over all T forecasts, should be close to zero. The standard normally distrib-
uted forecast breakdown test statistic is
where γj is a Newey-West estimator of the variance of the weighted losses.
Clearly, the precision of the estimate of the forecast model depends on the length
of the sample that is used for estimation. The null hypothesis of a forecast break-
down is rejected at significance level α whenever the forecast breakdown test
statistic is larger than the (1-α) -th quantile of a standard normal distribution.
FBjh =
j-jh
sl
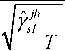
(3.10)
8 We only perform a one-sided test to reflect the assumption that a loss that is smaller than
expected is desirable and therefore does not constitute a forecast breakdown. The forecasting
scheme is recursive.
More intriguing information
1. The name is absent2. Real Exchange Rate Misalignment: Prelude to Crisis?
3. Nonlinear Production, Abatement, Pollution and Materials Balance Reconsidered
4. From music student to professional: the process of transition
5. The name is absent
6. Motivations, Values and Emotions: Three Sides of the same Coin
7. WP 1 - The first part-time economy in the world. Does it work?
8. New Evidence on the Puzzles. Results from Agnostic Identification on Monetary Policy and Exchange Rates.
9. The name is absent
10. Quality practices, priorities and performance: an international study