MICROWORLDS BASED ON LINEAR EQUATION SYSTEMS: A NEW APPROACH TO COMPLEX PROBLEM SOLVING AND EXPERIMENTAL RESULTS

J. Funke

(3) A detailed diagnostic procedure should reveal the subject’s development
of hypotheses about the system. This implies that subjects have to be
prompted repeatedly about the causal structure they assumed to the system.
(4) There should be a clear distinction between a phase of knowledge
acquisition (mainly realized by encouraging the subjects to explore the
system) and a phase of knowledge application in which certain states of the
problem space should be reached by the subjects as quickly as possible. In this
last phase, performance measures should precisely indicate the quality of a
subjects' intervention.

The DYNAMIS Shellfor Scenarios

Trivially, before you can control a complex system, you must Ieam how it
works. To study experimentally the acquisition, as well as the application, of
knowledge we confront our subjects with dynamic computer-simulated
scenarios. As a universal tool for constructing these scenarios a computer
program called DYNAMIS serves as a shell, with which the experimenter can
implement in a simple way different types of simulated systems which all
have in common one formal background. This general frame is a linear
equation system (see e.g., Steyer, 1984) which consists of an arbitrary number
of exogenous (=x) and endogenous (=y) variables according to the following
equation:

y^,+1=A∙y* + B*x^,                   (1)

where y*¹ and y^, are Vectorsrepreseniingthe state of the endogenous Variablesaitinies
t+1 and t; x^, is a vector representing the values chosen by the subject for the exogenous
variables; A, B are matrices containing the weights for the variables.

A set of measures for formally describing such systems has been suggested
(e.g., Hiibner, 1989). An equation system is constructed according to
theoretical considerations about the presumed influence of certain system
attributes on task complexity (e.g., the effect of Eigendynamik or the
influence of side effects or effects due to different interdependencies). It is
not intended to simulate a domain of reality adequately, because that kind of
simulation puts too many constraints on the attributes of the system to be
useful for basic research on problem solving. Consequently, most of the
simulated systems used in our research group have been “artificial”. With
respect to a distinction made by Hays and Singer (1989) one can say that what
we want our systems to possess is not physical fidelity, but rather functional
fidelity. As an example see the SINUS system shown in Fig. 1.

Chapter 14 Microworidt Based on Linear Equation Systems

Subjects are told that this fictitious system consists of living creatures from
a distant planet called SINUS. The “endogenous” variables are introduced as
creatures labeled “Gaseln” (y,), “Schmorken” (y₂) and "Sisen” (y_j), the

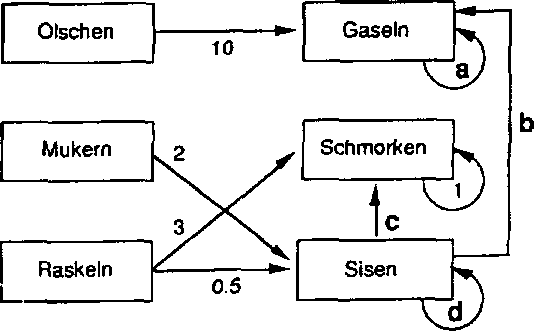
Figure 1: Causal structure σfthesystem SINUS. Theweight parametersinihestandard
configuration are set to a=l, b=0, c=0.2, and d=0.9, but are changed due to
the experimental purposes.

“exogenous” creatures are called “01 sc hen” (x₁), “Mukem" (x₃) and “Raskeln”
(χ₃). The system has the following structure (parameters a, b, c, and d
represent variable weights, with a=l, b=0, c=0.2, and d=0.9 being the standard
set):

у _l^w ≈ 10.0 ∙ x_l' + a ■ y₁^l + b ∙ y_j',
y>^,+l = 3.0 ■ x₃¹ ÷ LO ∙ y₃^t + c ∙ y₃^l,
y₃^,∙' = 2.0 ■ x√ + 0.5 ∙ x_j^, + d ∙ y₃'

The task for the subjects is first to explore the system (i.e., to find out the
causal links between tħesystem variables) and then to control the endogenous
variables (=the numbers of у-creatures) by means of the exogenous variables
with respect to a set of given goal states. Parameters a to d are manipulated
depending on the experimental conditions (see below).

<<   <   1   2   3   4   5   6   >   >>