A trained ANN implements a mapping from the input
nodes (I1-n) to the output nodes (O1-i). The power of
the ANN is in its ability to implement some function
O1-i = f(I1-n)
from the training data set. Hoffmann (1998) emphasizes
this point and says that
[t]he greatest interest in neural nets, from a prac-
tical point of view, can be found in engineering,
where high-dimensional continuous functions need
to be computed and approximated on the basis of a
number of data points (Hoffmann, 1998, 157).
The modeler does not need to specify the function
f , in fact, the modeler does not even need to know
anything about f. Knowledge extraction (KE) from
ANNs is concerned with providing a description of the
function f that is approximated by the trained ANN.
The extraction of the function “lies in the desire to have
explanatory capabilities besides the pure performance”
(Hoffmann, 1998, 155). The ability to determine f may
or may not add to the explanatory value of the model.
For moderately sized networks and relatively simple
functions it is quite feasible to describe the model in a
series of simple logic statements or with some high level
programming language. In this step by step description
of the network in terms of its input-output relations,
knowledge of the function that will be ultimately
implemented is not necessary. A particular relationship
could be expressed, albeit awkwardly, in the form
if I1 = 0 and I2 = 1 then On = 1
else if I1 = 1 and I2 = 0 then On = 1
else if I1 = 1 and I2 = 1 then On = 0
else if I1 = 0 and I2 = 0 then On = 0
The simple XOR-function is easily recognized in
this example. This approach may not be practical for
more complicated functions, however it would be possi-
ble in principle. ANNs can even offer a convenient way
of implementing complicated functions approximately,
if some data points of these functions are known. The
number of data points that are available for the training
of the network determine how close the approximation
of the functions can be, unless the function is known
to be linear. The ability to process even relatively
large data sets make ANNs valuable analytical tools to
reveal something about the data. Even employing KE
methods that may help to determine the function f
does not overcome the limitation that the ANN cannot
deliver anything new for the cognitive model. Regres-
sion analysis (curve fitting) performed on the training
dataset will provide a more exact description of f than
to teach an ANN and to perform KE subsequently.
There is a further complication as the data revealed in
the cluster analysis is not accessible within the model.
In other words, the results of the analysis are not fur-
nished by the ANN. Rather, they are interpretations of
the internal structures at a different level of description.
The actual role of the network is that of a predictor,
where the trained network attempts to guess the next
output following the current input11 . The analysis of
the experiment is framed in the language of the higher
cognitive function that is the sub ject of the model.
For the interpretation and the analysis of the results,
the output nodes are neglected and new ‘output’ for
the model is generated by methods that belong to a
higher level of description than the ANN. New ‘insights’
are synthesized from distributed representations by
means and methods external to the ANN. Figure 3
illustrates the disconnectedness of the ANN and the
newly gained ‘insights’ emerging from the network’s
internal representations. The experimenter performs
the task of extracting information about the activation
pattern using a new tool, cluster analysis for example,
however the network has no part in this - ANNs do not
perform cluster analysis. The work is clearly performed
by the modeler’s neurons with the aid of a statistical
procedure and not by the model’s neural structure.
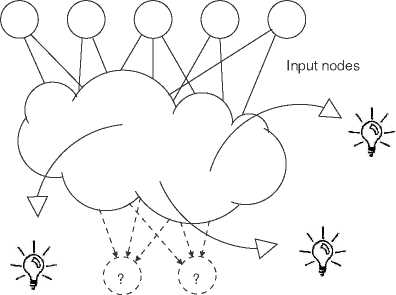
Figure 3. Actual model architecture
If the ANN is meant to be a model of what might happen
at the neural level, then the question arises, what mech-
anism could be responsible for the equivalent (cluster)
analysis of activation patterns in the brain? In order to
make this information accessible to the rest of the brain,
we will have to introduce some other neural circuit to do
such an analysis of the hidden nodes. Such a new addi-
tion to the network could possibly categorize words into
verbs and nouns, but then we need another circuit to
categorize words into humans, non-humans, inanimates,
or edibles, and another to categorize words into mono-
syllabic and multi-syllabic. In fact, we will need an very
large number of neural circuits just for the analysis of
word categories, provided the training dataset contains
the appropriate relations to allow for such categoriza-
tions.
The class of simple ANNs that I have discussed here can-
not provide any new ‘insights’ in any meaningful sym-
bolic12 or coded form on some output nodes. This, how-
ever, would have to be a crucial function of the model
11The desired output, which follows the input in the train-
ing set, is used as the target to determine the error for back
propagation during the training phase.
12I do not think that ‘distributed’ or ‘sub-symbolic’ rep-
resentations are helpful here. Moreover, this alternative ap-
1188
More intriguing information
1. Aktive Klienten - Aktive Politik? (Wie) Läßt sich dauerhafte Unabhängigkeit von Sozialhilfe erreichen? Ein Literaturbericht2. TOWARD CULTURAL ONCOLOGY: THE EVOLUTIONARY INFORMATION DYNAMICS OF CANCER
3. HOW WILL PRODUCTION, MARKETING, AND CONSUMPTION BE COORDINATED? FROM A FARM ORGANIZATION VIEWPOINT
4. Testing Panel Data Regression Models with Spatial Error Correlation
5. Effort and Performance in Public-Policy Contests
6. Direct observations of the kinetics of migrating T-cells suggest active retention by endothelial cells with continual bidirectional migration
7. Spectral density bandwith choice and prewightening in the estimation of heteroskadasticity and autocorrelation consistent covariance matrices in panel data models
8. Placentophagia in Nonpregnant Nulliparous Mice: A Genetic Investigation1
9. The Clustering of Financial Services in London*
10. Factores de alteração da composição da Despesa Pública: o caso norte-americano