IJCSI International Journal of Computer Science Issues, Vol. 2, 2009 50
classifiers are combined using matching scores. Section 3
presents feature extraction using canonical form based on
PCA. Section 4, the individual traits are fused at matching
score level using sum of score techniques. Finally, the
experimental results are given in section 5. Conclusions
are given in the last section.
2 System Structure
The multimodal biometrics system is developed using two
traits (face & palmprint) as shown in the figure1. For both,
face & palmprint recognition the paper proposes a new
approach called canonical form based on PCA method for
feature extraction. The matching score for each trait is
calculated by using Euclidean distance. The modules
based on individual traits returns an integer value after
matching the templates and query feature vectors. The
final score is generated by using the sum of score
technique at fusion level, which is then passed to the
decision module. The final decision is made by comparing
the final score with a threshold value at the decision
module.
3 Feature Extraction Using Canonical
Form Based on PCA Approach
The “Eigenface” or “Eigenpalm” method proposed by
Turk and Pentland [5] [6] is based on Karhunen-Loeve
Expression and is motivated by the earlier work of
Sirovitch and Kirby [7][8] for efficiently representing
picture of images. The Eigen method presented by Turk
and Pentland finds the principal components (Karhunen-
Loeve Expression) of the image distribution or the
eigenvectors of the covariance matrix of the set of images.
These eigenvectors can be thought as set of features,
which together characterized between images.
Let a image I (x, y) be a two dimensional array of intensity
values or a vector of dimension n. Let the training set of
images be I1, I2, I3, In. The average image of the set is
defined by
n
Ψ = -1 ∑ I i
N ⅛
(1)
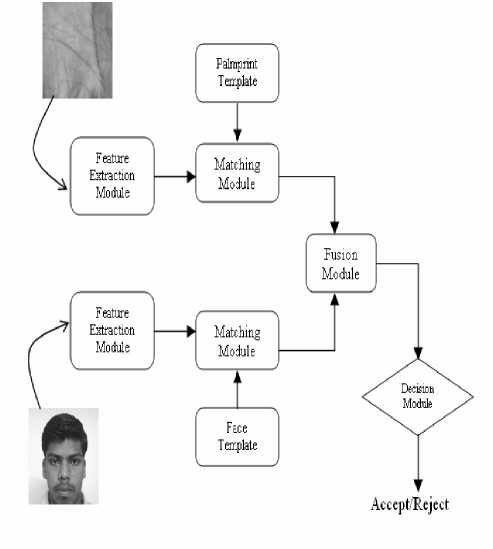
Figure1. Block diagram of face and palmprint multimodal biometric
system
Each image differed from the average by the vector. This
φ I = I i - Ψ set of very large vectors is subjected to
principal component analysis which seeks a set of K
orthonormal vectors Vk, K=1,......., K and their associated
eigenvalues λk which best describe the distribution of
data. The vectors Vk and scalars λk are the eigenvectors
and eigenvalues of the covariance matrix:
1N
C = N ∑ φ φ = A A’
(2)
Where the matrix A = [φ1, φ 2...........φ N ] finding the
eigenvectors of matrix Cnxn is computationally intensive.
However, the eigenvectors of C can determine by first
finding the eigenvectors of much smaller matrix of size
NxN and taking a linear combination of the resulting
vectors [6].
The canonical method proposed in this paper is based on
Eigen values and Eigen vectors. These Eigen valves can
be thought a set of features which together characterized
between images.
Let Q be a quadratic form given by
nn
Q = C ’ I C = ∑∑ a ij ci c j (3)
i=1 j-1
IJCSI
More intriguing information
1. Evaluating the Success of the School Commodity Food Program2. Outline of a new approach to the nature of mind
3. The name is absent
4. The name is absent
5. The Triangular Relationship between the Commission, NRAs and National Courts Revisited
6. The name is absent
7. The Complexity Era in Economics
8. A THEORETICAL FRAMEWORK FOR EVALUATING SOCIAL WELFARE EFFECTS OF NEW AGRICULTURAL TECHNOLOGY
9. The ultimate determinants of central bank independence
10. The name is absent