the derivation is presented for a pure fluid of branched chain molecules having m
backbone segments and two branches at backbone segments ‘j’ and lk,, as shown in
fig. 7.la. The branch at ‘j’ has mj- segments enumerated as bj-l, bj2, ..., bjmj. This
notation is used to distinguish the branch segments from the backbone segments. The
generalization to chains with multiple branches will follow.
(a)
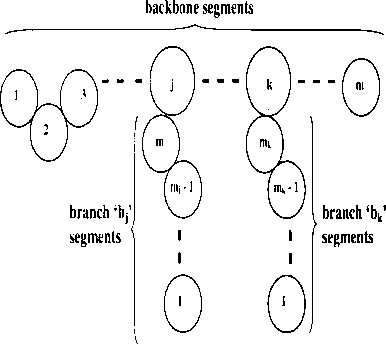
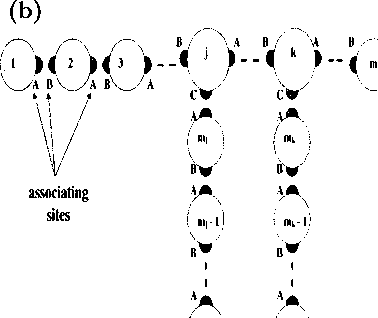
Figure 7.1: (a) Model of a branched chain molecule. The backbone has ‘m’ segments and
the two branches at backbone segment ‘j’ and ‘k’ are ‘b/ and ζb∕c,, respectively, bj has mj
segments while bʌ, has n⅛ segments. The total number of segments in the chain, N = m
+ mj∙ + rn⅛. (b) Schematic of the formation of a branched polymer chain of N segments
from N associating spheres. For a middle segment a , site ‘A’ associates with site ‘B’ on
the segment a' = a + 1 and site ‘B’ associates with site ‘A’ on the segment a' = a - 1.
The branch points on the backbone T and ‘k’ have additional associating site ‘C’ which
associates with the branch segments, 1bj m3, and ζb⅛ m⅛,, respectively. End segments 1, m,
tb7 1’ and ‘bfc 1’ have only one associating site, ‘A’ or ‘B’.
The grand free energy (Ω) of the chain fluid at fixed volume ( V), temperature ( T),
and chemical potential (μ) in the presence of an external field ( Vearf(R)) is related to
184
More intriguing information
1. Public-Private Partnerships in Urban Development in the United States2. Change in firm population and spatial variations: The case of Turkey
3. The name is absent
4. THE UNCERTAIN FUTURE OF THE MEXICAN MARKET FOR U.S. COTTON: IMPACT OF THE ELIMINATION OF TEXTILE AND CLOTHING QUOTAS
5. Cryothermal Energy Ablation Of Cardiac Arrhythmias 2005: State Of The Art
6. The name is absent
7. The name is absent
8. The Triangular Relationship between the Commission, NRAs and National Courts Revisited
9. XML PUBLISHING SOLUTIONS FOR A COMPANY
10. Rural-Urban Economic Disparities among China’s Elderly