directional attraction sites as shown in figure 3.1. From TPTl, the free energy func-
tional for such a system of associating hard spheres can be written as a perturbation
to the reference hard sphere fluid.
A[p(r)] = A⅜(r)] + Λ≡λs∏γ)] + A≡^'soc[p(r)] (3.7)
where A2d[p(r)] is the ideal gas free energy, A'εx,7ω[p(r)] is the contribution to the
free energy due to the reference fluid of hard spheres and is approximated using
the weighted density functional developed by Tarazona [107]. j4f'x,'ωsoc[p(r)] is the
contribution to the free energy due to association and can be written from Chapman
et. al. [58].
= ∑ / drp(t) I 1пХд(г)
Λ∈Γ∙' ×
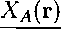
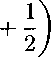
(3.8)
where -Хд(г) is the fraction of atoms not bonded at site A and the sum is over all the
sites. '
X√r1) l + ^BerKghs(a-,Pbulk)fABfdr2p(r)XB(r2)' (3'9)
where K is a geometric constant which depends upon the bonding volume, g>ιs is
the hard sphere correlation function, and fAB is the association Mayer /-function
(averaged over all configurations of sites A and B),
∕ab —
(1 - cos0c)2
4
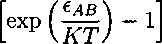
(3.10)
69
More intriguing information
1. The name is absent2. Inhimillinen pääoma ja palkat Suomessa: Paluu perusmalliin
3. Institutions, Social Norms, and Bargaining Power: An Analysis of Individual Leisure Time in Couple Households
4. Demand Potential for Goat Meat in Southern States: Empirical Evidence from a Multi-State Goat Meat Consumer Survey
5. Moi individuel et moi cosmique Dans la pensee de Romain Rolland
6. The Economics of Uncovered Interest Parity Condition for Emerging Markets: A Survey
7. Developments and Development Directions of Electronic Trade Platforms in US and European Agri-Food Markets: Impact on Sector Organization
8. Inflation and Inflation Uncertainty in the Euro Area
9. The name is absent
10. A Note on Productivity Change in European Co-operative Banks: The Luenberger Indicator Approach