The name is absent

72

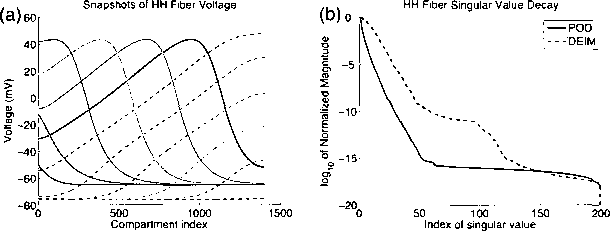
matrices as in (3.2.1), we find that they decay quite rapidly (see Figure 3.1B), thus it
is reasonable to expect that a small reduced system can approximate the full system
well.

(C)

130μm

18    11   7   15 3 13 8 17 4    10 5 20 14 2 16 9     6 12 19 1

Figure 3.1: (a) Sample traces of voltage snapshots used to construct the HH fiber reduced
system. Shown are snapshots 22:10:132 of the simulation, (b) Decay of singular values for
the POD and DEIM bases for the HH fiber, (c) Location of the first 20 DEIM points on
the fiber, indexed by order in which they were computed.

Note that the decay of these singular values to some tolerance does not necessarily
imply a corresponding accuracy of the reduced system as compared to the full one.
As shown in §2, for linear systems there exist SVD-based model reduction methods,
such as Balanced Truncation, for which rigorous error bounds exist in terms of the
decay of Hankel singular values (Glover, 1984) (Antoulas and Sorensen, 2001), and
these have been successfully applied to the linearized version of (2.17) (Kellems et al.,
2009). For nonlinear systems the reduction relies upon having a good snapshot set.
Hence if the snapshot set is poor, then the decay of the singular values need not be
indicative of the existence of a good reduced system. However, if the snapshot set is

<<   79   80   81   82   83   84   85   >>

More intriguing information