The name is absent

31

3.4.2 Large-N System Simulation

Another important objective as we have stated is about the finite-size effect. To characterize
the experiments correctly, we need to push the calculated particle number to the order of
10⁵. In doing so, we can examine whether if the topological structures we observed in
small-N system still exist and could be the sign of the FFLO state. For this purpose, we
are going to use an ideal model in which the polarized Fermi gas in a 2D harmonic trap in
the X-Y plane while we impose a periodic boundary condition in the Z direction. With this
setup, we expect to reduce the computation time significantly and eliminate the finite-size
effect to examine whether the FFLO-Iike oscillatory structures we observed above indeed
represents a real bulk FFLO phase.

3.4.3 Time-dependent BdG Simulation

Besides improving on the algorithm, we are looking to expand the function of our code
to apply it to investigate new scenarios. Solving the time-dependent BdG numerically is a
powerful tool for investigating the dynamical properties in Fermi gases as in the BECs, or
seeking the ground state by evolving in the imaginary time as we have done in Chapter 2.

Basically the time-dependent BdG can be written as

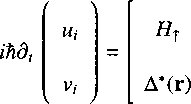
The time-dependent version BdG equation can be solved with the split-step Fourier
scheme that we discussed in the previous chapter. However the standard procedure needs

<<   37   38   39   40   41   42   43   >>

More intriguing information