The name is absent

Lectures on Scientific Subjects

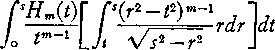
so that we have

^{(6) mj}>^⅛ Γ.'3.∙'^2,-l ¾S∕'⅜r(^j,-^i,)-*^d∙]

Now we may differentiate m times as to ʃ under the integral
sign because the integral and its first m — 1 derivatives
vanish for t=s. Writing then s—tu in that u≥l we obtain
the equivalent form

1            7^w /7 f^s rj^rn

(6^,) λ_mω=τ- <-- o  о—г τ

⁴            2τr 1 ∙3 ∙ ∙ ∙2m — 1 ds J_o      du^m

But it is readily proved by induction that

(m+√ w² — l)^m — (m — V u²~l)^m

Substituting, we obtain the stated final explicit formula

/04 _й /4 d^m dV [^,τr ,Λu+∖∕u^s-l)^m+(u-Vuⁱ-l)^mj~]

(8) Us) =_ra[J_o H_m(t)        ^==_ι--------diJ

P

yielding the explicit Fourier coefficient ʌ,(ʃ), g_m(√) for
f(s, φ) in virtue of the formula A_m(j) =f_m(s) +⅛_m(j).

GEORGE D. BIRKHOFF.

<<   27   28   29   30  

More intriguing information