Appendix I: Wage and Employment Determination
The Bargaining Model
The bargaining problem is given by
max∣ L [((i -τ)wu )ρ- (B)ρ]∣ (Y - wuL -wsL )1 γ
wu < L )
(A.1)
The union takes into account the fact that, given the skilled wage ws, the reduction in L due to an
increase in wu will reduce skilled employment and hence the marginal product of skilled labour. The
resulting first-order condition is
wu
ρ-i
r
ρ(1 -τ)ρ+ (1 -τ)ρ
к
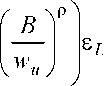
1 -γ L ((1 -τ)ρ wρ- ( bY )ρ )
γ Y - Hws - Lwu
(A.2)
Using the fact that
Y - Hws - Lwu _ 1 - θ
Lwuu ^ (1 -β)θ
we can write (A.2) as
ρ(1 - τ)ρ
—(1 -β) rθ→ε L
γ 1-θ
(
I (1 -τ)ρ

(A.3)
Comparative Statics
Consider first a number of comparative statics obtained from the production function. From equation
(1b), we obtain the elasticities of demand for the two types of labour
εL = -
∂L wu
∂wu L 1 -(1 -β)[θ(1 + σ)-σ]
(A.4)
εH = -
∂H ws
∂ws H 1 - β[θ(1 + σ) - σ]
(A.5)
From equations (1)-(5), (11), (12), (A.4) and (A.5) we have
sign
∂θ
= si
(A.6)
∂L<0,
∂ω<0,
∂H
∂wu<0,
∂L
∂ε
L > 0,
∂θ
∂H < 0,
∂ω>0,
∂L
∂K > 0,
∂ω<0,
∂h
∂wu
∂H
∂εH
∂θ
∂w ∂w ∂w ∂w
> 0, wu > 0, ws > 0, ws < 0, ws > 0,
∂K ∂L ∂H ∂K
> 0.
31
More intriguing information
1. Olive Tree Farming in Jaen: Situation With the New Cap and Comparison With the Province Income Per Capita.2. Popular Conceptions of Nationhood in Old and New European
3. EMU's Decentralized System of Fiscal Policy
4. Solidaristic Wage Bargaining
5. Non-farm businesses local economic integration level: the case of six Portuguese small and medium-sized Markettowns• - a sector approach
6. Dendritic Inhibition Enhances Neural Coding Properties
7. The name is absent
8. Existentialism: a Philosophy of Hope or Despair?
9. Improving Business Cycle Forecasts’ Accuracy - What Can We Learn from Past Errors?
10. The name is absent