linear income tax system with zero tax on contributions (s=0), we ask whether levying
a small tax (possibly negative) on charitable contributions would increase welfare.9
Denote the Lagrangean expression for the optimal income tax problem, given
a tax s on contributions, by:
(12)
wr
L(s) = W[V NS (w )]dF (w ) + μ1 1 t ∙
wc wc
∫ w [1 - Ins (w)]dF(w ) + (1 + s) ∙ ∫ zNS (w)dF(w) - g - T >
w w
K
∫ zNS ( w ) dF ( w )k
w
where μ1 and μ2 denote the Lagrange multipliers associated with the constraints in
equations (10) and (11). Employing the envelope theorem and omitting the NS
superscript for brevity of notation, we seek to sign the following derivative:
where t*,T* and g* denote the optimal tax parameters and λ(w) denotes the Lagrange
multiplier associated with the individual optimization.
(13)
∂L
_ ж л ж
∂s s=0,t*,T*,g*
[W ' [V ( w )] ∙ λ( w ) ∙ z ( w )]dF ( w ) - μ1 ∙ t ∙
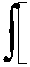
dF ( w )
+ μ1 ∙
w
w
ʃ[z ( w )]dF ( w ) + ( μ1 - μ2) ∙
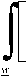
dF ( w ),
There are two conflicting considerations in the design of the optimal
tax/subsidy on charitable contributions. On the one hand, there is a Pigouvian motive
to subsidize contributions, because they generate a positive externality. This is due to
9 Assuming that second order conditions are satisfied, this would imply that the optimal tax on
contributions should be positive (negative), if a small tax (subsidy, respectively) is shown to be
desirable.
13