Temporary Work in Turbulent Times: The Swedish Experience

30

increase in θ^P in the sense that it requires a bigger increase in profitability (decline in wages or increase
in productivity) to maintain zero profits on new vacancies. The reason is that a rise in the expected
duration of vacancies, 1/q(∙)^j = (θ^j )^η, is more costly the higher the separation rates are. Clearly, only
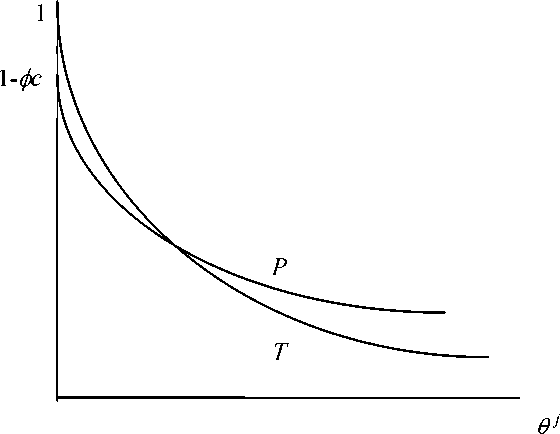
temporary contracts will be offered for w/y > 1 -φc ;as w/y falls below 1 -φc , permanent contracts are
also offered. As illustrated in the figure, the demand for permanent contracts may eventually exceed the
demand for permanent contracts for sufficiently high rates of profitability.

Figure A1. The Demand for Temporary and Permanent Contracts.

w/y

By using (A1) and (A2) we can express the ratio between vacancies pertaining to temporary and
permanent contracts as follows:
where we have used the fact that θ^T /θ^P = v^T /v^P . Note that this relative vacancy ratio is increasing in
w/y, i.e., decreasing in profitability. To obtain an expression involving the number of employed workers
we use the flow equilibrium relationships. For temporary jobs we have: q^Tv^T = λT , where T is the
number of workers on temporary contracts. For workers on permanent contracts the analogous expression
is: q^pV = λP . We thus obtain: T/P = (φ/λ)(v^τ /v^p)^1-η . It is clear that the ratio T/P (as well as

φc

1 - φc - ( w / y )

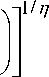
TP

v / v ) is declining in profitability.

<<   30   31   32   33   34   35   36   >>

More intriguing information