Figure 2: Expected utility as a function of the severity of the illness
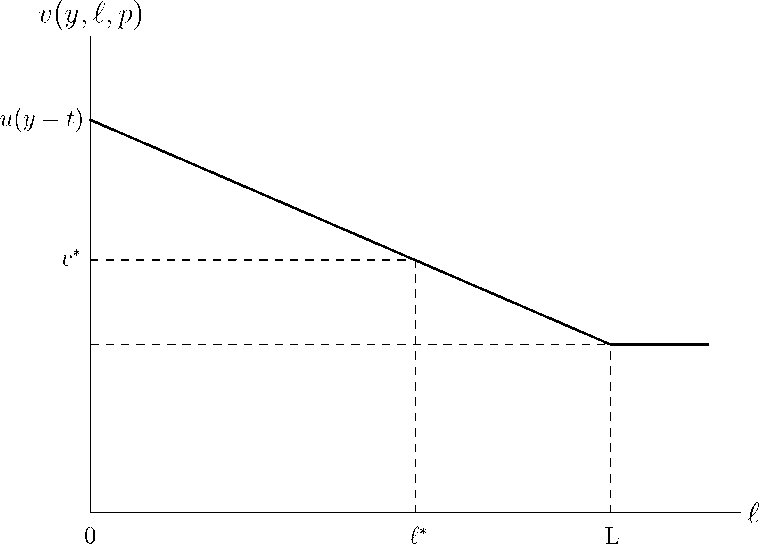
Δ = H⅜)>'(y — t) У δ(u)dF(y, €)
— [1+ t'(p)]u'(У — t — P) 2" δ(υ)dF(y,€) (15)
Moreover, (13) can in this case be written as
ʃ δ(υ)dF(y,€) = ʃ δ(υ)dF(y,€) < 0
(16)
since δ(v) > 0 for € > L. The first integral in (15) is in other words negative.
The second integral in (15) is positive, since δ(v~) > 0 for € > L. Since the
terms [—t'(p)] and [1 + t'(p)] are both positive, it follows that Δ < 0 in the
present case. From our previous discussion we thus have the the following
proposition:
10
More intriguing information
1. Pricing American-style Derivatives under the Heston Model Dynamics: A Fast Fourier Transformation in the Geske–Johnson Scheme2. Dynamic Explanations of Industry Structure and Performance
3. The name is absent
4. Segmentación en la era de la globalización: ¿Cómo encontrar un segmento nuevo de mercado?
5. The ultimate determinants of central bank independence
6. The demand for urban transport: An application of discrete choice model for Cadiz
7. Cryothermal Energy Ablation Of Cardiac Arrhythmias 2005: State Of The Art
8. Evidence on the Determinants of Foreign Direct Investment: The Case of Three European Regions
9. Eigentumsrechtliche Dezentralisierung und institutioneller Wettbewerb
10. Learning-by-Exporting? Firm-Level Evidence for UK Manufacturing and Services Sectors