3. New Open Economy Macroeconomic Model
two individual goods z, z0 produced within a country σC(z),C(z0) equals θ (CES specification, θ > 1 for an
equilibrium to exist).9
The total domestic CPI is again a Cobb-Douglas composite of domestic and foreign producer price indexes
(PPIs):
(5)
n 1-n
Pt = Pt,H Pt,F ,
whereupon these subindexes are CES composites of domestic and foreign final goods prices:
Pt,H
Pt,F
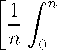
Pt(z)1-θdz
1 -θ
ɪ [1 Pt(z)1 -θdz
1-n n
(6)
(7)
For a derivation of the domestic CPI (5), the domestic PPI for domestic goods (6) as well as the domestic
demand functions for individual and composite domestic goods, which will be introduced below, see
Appendix A.1. The domestic PPI for foreign goods (7), domestic demand curves for individual and
composite foreign goods as well as all foreign indexes can be derived analogously.
Assume that the law of one price holds for consumers across all individual goods at all times:
Pt(z) = StPt (z)∀z ∈ [0, 1], (8)
where S denotes the endogenously determined nominal exchange rate in price quotation (domestic cur-
rency units in terms of foreign currency units).
Thus, as domestic and foreign households are characterized by identical preferences, the law of one price
implies that absolute purchasing power parity (PPP) always holds for the total CPI, even if relative PPP
(stating that changes in domestic and foreign price levels should be equal in the long run) would be the
more realistic statement (see Obstfeld/Rogoff 1996, pp. 200-202):
Pt = StPtt . (9)
The demand functions of the representative domestic household for individual domestic C(h) and foreign
goods C(f) read as follows:
-θ
Ct(h)
Ct(f)
Ct,H,
1-n
'P( ( f ) ■
_ Pt,F _
Ct,F,
(10)
(11)
where z = h ∈ [0, n] denotes a typical differentiated good z produced at home and z0 = f ∈ (n, 1] another
typical differentiated good z0 produced abroad.
As one can see from equations (10) and (11), demand for individual goods is decreasing in its own price
'σ'"H, Cf | :
d(HH\ dCH
CF dCF
,ddCh∖ Ch
d(dCHJ CH
=1,
lσc (z) ,C (z') | : =
d Γ C(z)- ]
d LC ( z' )J
d hd C ( z ) i
d[d C ( z' )J
d C ( z )
d C ( z' )
C ( z )
C (z' )
= θ.