114
M. Tirelli
equilibrium). In Fig. 2(b) below, we plot the aggregate (indirect) utility level
as a function of the return from holding the firm in state 1 (i.e., θ1y1), and
fixed x0, when allocations are feasible in the sense of Diamond. It is im-
mediate that the minimum welfare is obtained at the symmetric allocation,
while the only two CPO are corner solutions. Thus, Fig. 2(b) shows that
at a minimum welfare point, the symmetric equilibrium is a local CPO-
equilibrium: a Pareto superior equilibrium can be achieved by a Diamond
central planner via discrete portfolios and production reallocations.
- Optimal tax reforms 1. (Interior equilibrium) We start from the interior
equilibrium, and assume that a tax reform, such as the one considered in
Example 1, is introduced: dt1 = (-1, -5) %. Then a Pareto improvement
is obtained with a .04% increase in the utility of both agents, and an 4.17%
increase in the share of agent 1 in the firm:
|
% Ax 0 |
% Ax ] |
% Ax 2 |
% Aθ |
% Au | |
|
h=1 |
-7.86 |
1. 06 |
1.98 |
4.17 |
.04 |
|
h=2 |
7.86 |
-1. 06 |
-1.98 |
-4.17 |
.04 |
2. (Corner equilibria) Since the two corner equilibria are symmetric, we
consider only the one in which consumer 1 is the single owner of the firm.
The tax reform dt1 = (.1, 0) % is weakly Pareto improving:
|
% Ax 0 |
% Ax ] |
% Ax 2 |
% Aθ |
% Au | |
|
h=1 |
-.05 |
0.5 |
0 |
0 |
.06 |
|
h=2 |
0.5 |
-0.5 |
0 |
0 |
0 |
In words, a (global) CPO equilibrium can be improved upon by using pro-
portional income taxes.
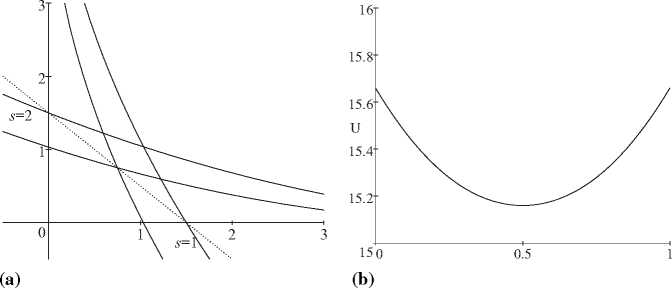
Fig. 2.