Published in Nunes,T (ed) Special Issue, ‘Giving Meaning to Mathematical Signs: Psychological,
Pedagogical and Cultural Processes‘ Human Development, Vol 52, No 2, April, pp. 129-
The pair began the task by creating a quadrilateral ABCD consisting of 4 line
segments arranged in no particular configuration. After labelling the four vertices,
they added the angle bisectors of angles ABC and BCD, and used the angle-
measuring tool to measure the angle where these two lines crossed. They then
carefully dragged the vertices of the quadrilateral until this angle measured 90° (see
Figure 1). Thus the constraints of the required quadrilateral were not constructed - i.e.
the angle between the bisectors could be easily shifted from 90o - but simply created
—by eye”. However, at the moment when the angle between the two bisectors in fact
measured 90°, the pair noticed that BA was parallel to CD. There was no doubt in
their minds, although they had, at that time, no validation of this hypothesis.
Nonetheless they immediately conjectured, on the basis of this one example, that
whenever the two angle bisectors were at right angles, BA must be parallel to CD. 1.
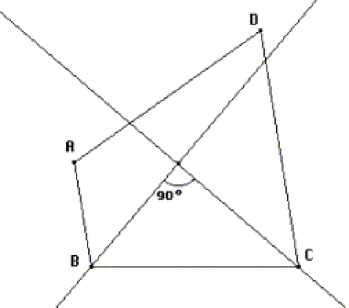
Figure 1: Sketching a quadrilateral with angle bisectors of two adjacent angles at right angles.
Such a conjecture can be designated as an abduction2. An abduction is
characterised by noticing a local commonality, which depends on a recognition, or
decision, about what counts as the same and different. This is subsequently
generalised by identifying the constraints or structural relationships that appear to
have given rise to the commonality (Radford, 2001): contrast with deduction that
involves inferring what must follow from a set of structural constraints.
1 Later, they went on to verify their conjectures in particular cases, explain why they must be
true in an informal way, and finally wrote a deductive proof based on their experimentation.
2 Arzarello, Micheletti, Olivero, & Robutti, 1998 also note how abduction is often used at the
conjecturing stage with Cabri.
More intriguing information
1. The name is absent2. Mean Variance Optimization of Non-Linear Systems and Worst-case Analysis
3. Credit Market Competition and Capital Regulation
4. Towards a Strategy for Improving Agricultural Inputs Markets in Africa
5. The name is absent
6. Cross border cooperation –promoter of tourism development
7. MATHEMATICS AS AN EXACT AND PRECISE LANGUAGE OF NATURE
8. Endogenous Heterogeneity in Strategic Models: Symmetry-breaking via Strategic Substitutes and Nonconcavities
9. CURRENT CHALLENGES FOR AGRICULTURAL POLICY
10. SLA RESEARCH ON SELF-DIRECTION: THEORETICAL AND PRACTICAL ISSUES