vais [âi-1,ai] for each sector i.
P =
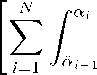
P}-θ df
1-θ
This can be further broken down into intervals for each cohort, where we
note that all firms in the same cohort face the same wage and hence set the
same price Pf = pij for f ∈
λ λ
âi-1 + ^ij-1ai, âi-1 + λijai
_N_ Ni_ f⅛i-1 +Ej ai
EE .. Pi- df
„•—i z,∙-i Jαi-ι+λij∙-ιαi
Li=1 j=1
1-θ
(8)
We can log linearize the price equations around the steady state , given the
wages. All firms with the same wage will set the same price: define Pij∙ as
the price set by firms in sector i cohort j. This yields the following log-
linearization in terms of deviations from the steady state (where we assume
P * = 1):
N N,
P = ∑ Σ "iʌijPij (9)
i=1 j=1
Note that there is an important property of CES technology. The demand
for an individual firm depends only on its own price and the general price
index (see 3). There is no sense of location: whilst we divide the unit interval
into segments corresponding to sectors and cohorts within sectors, this need
not reflect any objective factor in terms of sector or cohort specific aspects
of the technology. The sole communality within a sector is the length of
the wage contract: the sole commonality within a cohort is the timing of the
contract. The vectors a and λi are best be thought of as simply measures
of sector and cohort size. This is an important property which will become
useful when we show that a Calvo economy can be represented by a GTE.
2.2.1 Household-Unions and Wage Setting
Households h ∈ [0,1] have preferences defined over consumption, labour, and
real money balances. The expected life-time utility function takes the form
Uh = Et
e ot fr, Mht
/ j β u∖Cht, P ,
1_JHht )
Lht
(10)