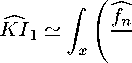
_
g
g
dFbn -
1 [ c- - g
2 7x∖ g
dFbn = KcI11
1
2 K112,
(18)
where KI11 is a stochastic element that will affect the asymptotic distribution of KI, while KI12 is roughly
the sum of squared bias and variance offcn . It is O((nh)-1 + h4) and it will contribute to the asymptotic
mean of KI.
15
2) KI2 has a different nature: it represents the part of the KI that is affected by the parameters estimation.
KI2 can be rewritten in the following way:
—
KcI2
(ln fbθ
x
ln fθ* )dF- + ( (ln fθ.
x
- ln g(x))dFbn =KcI21+KcI22.
(19)
Although in this case, the first term KI21 is stochastic, it will not affect the asymptotic distribution of
KI. In fact, since it is Op (ɪ) when rescaled by the appropriate convergence rate dn = nh1/2 it converges to
zero:
dn KI21 -→p 0. (20)
The second term KI22 has the following behavior:
—~-.
KFI22 -→ Eg [ln fθ. - ln g(x)] = (-KI(g, fθ )) ≤ 0, (21)
as such its presence is due to the approximation error. It is important to note that KI22 varies with the
underlying candidate model and it can not be observed. This implies that a term of the KcI’s asymptotic
mean will depend on the specific model Mj , then in order to determine and estimate a limiting distribution
that is the same for all candidate models the following assumption is needed:
A6: KI22 ` αh1'2KI12. (22)
A6 requires that the mean of the approximation error is proportional to a quantity KcI 12 whose estimation
depends only on fcn, consequently it will not be influenced by any specific model fj (bθ, x). Further, when
h к n-β with β > 5, KI12 ~ C(nh) 1, then we obtain that:
d-KI22 ` d-αh1'2KI 12 -→ αC = Eg [ln fθ. - ln g(x)], (23)
where C is a known positive constant. Thus collecting all terms together:
1
KI ` KI11 - 2KI12 - [KI21 + KI22) , (24)
we have the next theorem:
THEOREM 3: Given assumptions A1-A6, and given that nh5 -→ 0 as n -→ ∞, then
nh1/2
1
KI + 2 KI12 + KI22
-→d N(0,σ2)
15In order to see this, it is just sufficient to rewrite KII12 as R
2
^fn-Ec+Efn-g^ d_Fn.
10
More intriguing information
1. Regional dynamics in mountain areas and the need for integrated policies2. Campanile Orchestra
3. The name is absent
4. The name is absent
5. The name is absent
6. The name is absent
7. The name is absent
8. Neural Network Modelling of Constrained Spatial Interaction Flows
9. Optimal Taxation of Capital Income in Models with Endogenous Fertility
10. The name is absent