Spectral calibration of exponential Lévy Models [1]

Spectral calibration of exponential Levy models ??

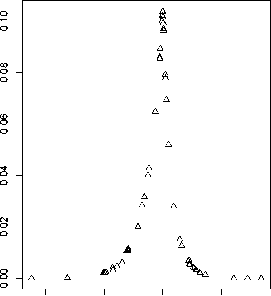
-2          -1           0           1

log-moneyness                                                   x

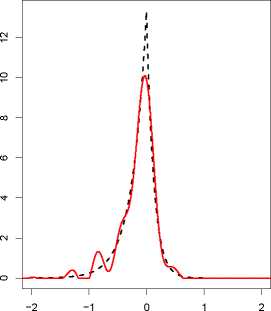
Fig. 1. Kou model. Left: Simulated option price data
Right: Calibrated Levy density ^ and true ν (dashed).

Both methods have certain distinctive features. In the PLS method the
penalisation plays a double role, it uses prior knowledge for the unknown
Levy triplet and it stabilizes the inverse problem. Because of the relative
entropy penalisation, the volatility σ is fixed in advance by the prior and
cannot be calibrated. In comparison, the spectral calibration (SC) method
profits from the regularity of the jump density for regularizing the inverse
problem. In particular, the volatility can be calibrated. The SC estimators
depend only on one critical tuning parameter, the cut-off frequency U , and
given U they are always uniquely defined.

In simulations the experience is that both methods yield roughly com-
parable results. The PLS method fits better the option price function, while
the SC method performs better in estimating the Levy triplet. The PLS
method has difficulties in estimating the jump density near zero, because
there are no smoothness constraints, while the SC method can yield nega-
tive values for jump densities, which should be corrected a posteriori, see
Belomestny and Reiβ (2006). Because it avoids a numerical minimisation
procedure, the SC method is considerably faster than the PLS method.

3.3. A numerical example

We consider the double exponential jump diffusion model proposed by Kou
(2002), where the Levy triplet is specified by the jump density

ν(x) = λ(pλ + e^{-λ + x} 1[o∞)(x) + (1 -p)λ-e^λ-x 1(-∞,ɑ)(x)´, x ∈ R, (20)
and the parameters σ, λ, λ+, λ- > 0 and p ∈ [0, 1], while γ is uniquely
determined by the martingale condition. We simulate the Kou model with

<<   7   8   9   10   11   12   13   >>

More intriguing information