A Consistent Nonparametric Test for Causality in Quantile

=∫K²(u)du∫f_z²(z)dz+o_p(1)

The result of Theorem (ii) follows from (A.31).

Proof of Theorem 1 (iii)

The proof of Theorem (iii) consists of the two steps.

Step 1. Show that JT = J_t + op (1) under the alternative hypothesis (4).

Step 2. Show that J_T=J+o_p(1) under the alternative hypothesis (4),

where J = E{[F_y^_z(Q_θ(x_t)∣ z_t)-θ]2f_z(z_t)} . The combination of Steps 1 and 2 yields
Theorem (iii).

Step 1: Show that J_t = J_t + op (1) under the alternative hypothesis.

We need to show that the results of Step 2 and Step 3 in the proof of Theorem (i) hold under
the alternative hypothesis. First, we show that the result of Step 2 in the proof of Theorem (i)
still holds under the alternative hypothesis. We can show that J₂(Q_θ - C_T)= o_p(1) by the
same procedures as in (A.24). Thus we focus on showing thatJ₂ (Q_θ) = o_p (1). As in the proof
of Theorem (i), denote S(g) ≡ ∂F[g] / ∂g . By taking a Taylor expansion of

Fy∣z^(qθ ^(xs )| ^zs ) ^{around q}θ ^(zs )^{, we have}

TT

∑ ∑

t=1 s≠t

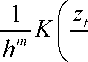
— z I

—s-∣{1(y_t ≤ Qθ(x_t)) -Fyz(Qθ(x_t)∣zt)}
h )

× ^{S (}Qθ ⁽x_s . ^zs ))

1^T

= -∑ {1(y_t ≤ Qθ(x_t)) — Fy∖z (Qθ (x_t ))}S(Qθ (x_s, zs)) f z(z_t)

T t=1

1^T

≡7∑ u,S(Qθ(x,,z,)).f (zt).

T t=1

where Q_θ(x_s,z_s) is between Q_θ(x_s) and Q_θ(z_s). By using the same procedures as in

19

<<   18   19   20   21   22   23   24   >>

More intriguing information