GR
US-Ger US-UK US-Japan
US/GE q ≥ 0
US/UK q ≥ 0
US/JP q ≥ 0
0 5 10 15 2 0 25 30 35 4 0 45 50 55 6 0
Months
0 5 10 15 20 a 3 3 40 45 5 » 60
Months
Grilli-Roub.
0 5 10 15 2 0 2 5 30 35 4 0 45 50 55 6 0
Months
US/UK q ≥ 0
US/JP q ≥ 0
0 5 10 1 5 2 0 25 30 3 5 4 0 45 50 5 5 6 0
Months
0 5 10 15 20 a a a 40 45 a a 60
Months
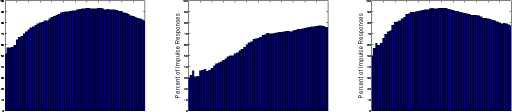
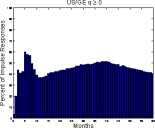
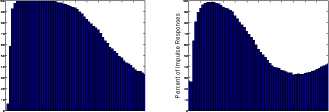
Figure 16: Distribution for the sign q ≥ 0 of the real exchange rate, condi-
tional on a foreign monetary policy contraction. We compare the benchmark
identification and imposing i* — i ≥ 0 in the GR VAR specification to the
BIG VAR specification as well as the recursive Grilli-Roubini identification.
GR
US-Ger
US-UK US-Japan
Grilli-Roub.
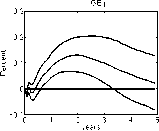
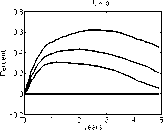
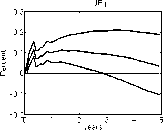
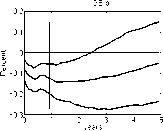
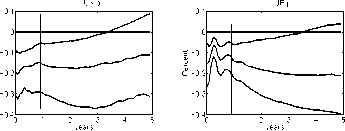
Figure 17: Impulse response function of the price level, conditional on a
foreign monetary policy contraction. We compare the benchmark identifica-
tion and imposing i* — i ≥ 0 in the GR VAR specification to the recursive
Grilli-Roubini identification. Note that there is a considerable price puzzle
in the Grilli-Roubini specification, which is avoided with sign restrictions by
construction.
51
More intriguing information
1. Estimating the Technology of Cognitive and Noncognitive Skill Formation2. The name is absent
3. The Advantage of Cooperatives under Asymmetric Cost Information
4. The name is absent
5. The name is absent
6. ANTI-COMPETITIVE FINANCIAL CONTRACTING: THE DESIGN OF FINANCIAL CLAIMS.
7. The name is absent
8. The name is absent
9. On the job rotation problem
10. THE CHANGING STRUCTURE OF AGRICULTURE