which also implies Π1H3 = p2H c0 (s)D1 > 0. The consequence is immediate from Prop.
1 and Prop. 3: while there may or may not be a strategic incentive to reduce transport
costs when there are barriers to entry abroad, under free entry, this incentive always
exists:
Proposition A2. When the number of firms is exogenous, there is (not) a strategic
incentive to reduce transport costs under strategic substitutability (complementarity),
but when there is free entry there is always a strategic incentive to reduce transport
costs.
Clearly the result applies also when the cost function is not linear but the policy
can reduce the marginal cost of transport. Moreover, the result naturally extends to
any form of export promotion which reduces some kind of costs for the exporting firms,
for instance labour cost, financial costs or taxation.
Appendix D: Optimal export subsidy under price
competition
In this Appendix I will show how to solve for the optimal trade policy in a model
of price competition with a demand function a la Dixit and Stiglitz (1977) with and
_ _ 1
without barriers to entry. Imagine a demand function for good i, Di = (pi/P) 1-θ ,
(∑n-ι p- ʌ)
1-θ
θ
where P ≡
is the price index. This can be derived from a utility
function (or a production function) where 1/(1 - θ) is the elasticity of substitution
between goods (inputs). Different firms produce the differentiated goods and engage
in price competition. To re-express this model in terms of our variables, let us set
θ
xi ≡ 1/pi and h(xi) = xi1-θ so that, in presence of a specific subsidy we have:
Π(xi ,βi ,si)=
xi1
-θ
- (c - si)xi -
_ 1
[h(xi) + βi] θ
(23)
It follows that Π12 > 0 at the optimal point satisfying Π1 =0, which implies strategic
complementarity, as customary under competition in prices, and Π13 > 0. This is not
by chance, since (23) can be seen as a particular case of (3).
Consider first the case of barriers to entry and an exogenous number of firms n.
In the exact solution, the price of the foreign firms p = p(s) and of the domestic firm
pH = pH (s) solve the system of equilibrium conditions:
1 2-θ
θpH1-θ - (c - s)pH 1-θ
. . θ -ɪ
(n — 1)p 1-θ + pH
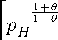
2
- (c - s)pH1 -
(24)
θθ- 1-θ
cp
2-θ ^l . χ
1-θ (n — 1)p
+ pH
θ
1 -θ
Γ 1+θ __2_
p 1-θ — cp 1-θ
(25)
26
More intriguing information
1. Can genetic algorithms explain experimental anomalies? An application to common property resources2. The name is absent
3. The name is absent
4. Strategic Effects and Incentives in Multi-issue Bargaining Games
5. Strengthening civil society from the outside? Donor driven consultation and participation processes in Poverty Reduction Strategies (PRSP): the Bolivian case
6. Effort and Performance in Public-Policy Contests
7. A Note on Productivity Change in European Co-operative Banks: The Luenberger Indicator Approach
8. An Incentive System for Salmonella Control in the Pork Supply Chain
9. The name is absent
10. The open method of co-ordination: Some remarks regarding old-age security within an enlarged European Union