The name is absent

Proposition 3.- Under A.3 we have that

a) U(I) ≥ U (2) and
1                 i

b) if x (2) > O then the above inequality is strict.

Proof : Suppose it is not. Defining V ( ) as before we have that
------------------ i

V (x (2)_i x (2)) ≥ V (x (I)_i O) ≥ V (x (2)_i O)
112   11    11

And since Vf ) is decreasing on x . we get a contradiction .■

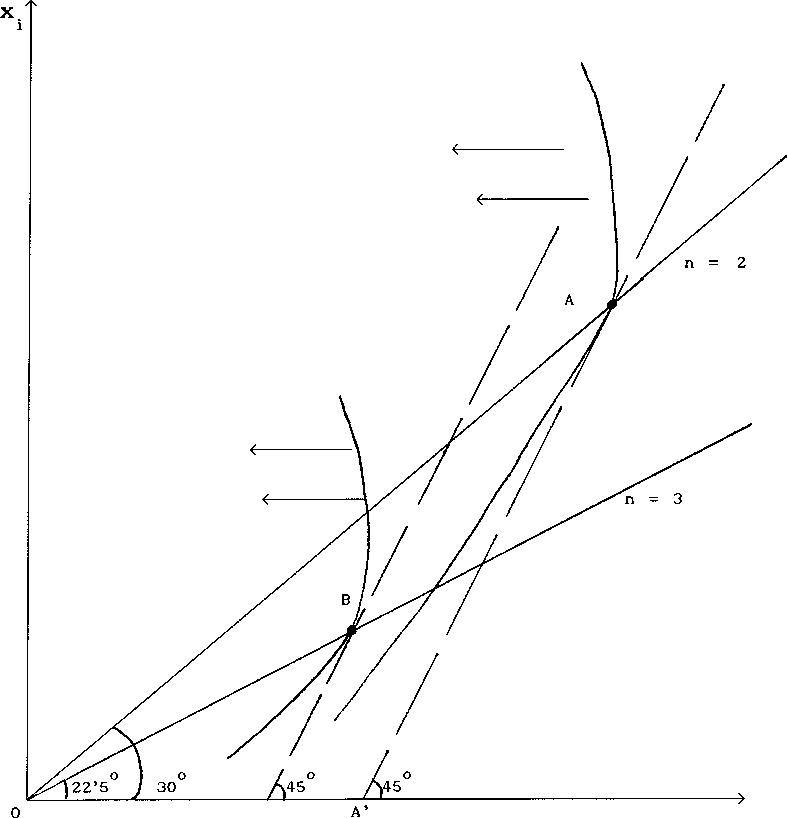
FIGURE 1

19

<<   15   16   17   18   19   20   21   >>

More intriguing information