12
PEDRO PABLO ALVAREZ LOIS
In summary, the household’s problem is to maximize (2.29) subject to (2.31)-(2.32)
by choice of contingency plans for {Ct, Dt, Lt}ζf0 given the stochastic process for
{ Pt, Pt, Wt, jRtb, P}l, ∏{, ∏t6} “ θ
with expectations formed rationally under the assumed information structure. More-
over, the household must respect the constraint O ≤ Mt - Dt ≤ Mt-ι.The first
order conditions to the previous problem are represented by a set of Euler equa-
tions together with some appropriate boundary conditions. Is is assumed that the
conditions for an interior solution are satisfied, and thus the cash in advance con-
straint (2.31) and the money stock equation (2.32) are binding. Next, I proceed to
summarize these conditions.
Lemma 4. The optimal behavior of the household is characterized as follows: the
optimal consumption and labor decisions are given by
(2.33)
Ull = Wt
Uct Pt
and the optimal portfolio choice
(2.34)
where Uc and Ul denote the partial derivatives of U with respect to C and L re-
spectively; from the Cash-in-Advance constraint, consumption is derived
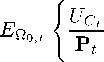
/3(1 + <) I7c,t+1
Pt+ι
35) Ct =
Pt
The formulation and results in this section are rather standard within the lit-
erature of limited participation models. Equation (2.33) governs the household’s
consumption and labor hour decision. Equation (2.34) is associated with the house-
hold’s portfolio decision. Note that the decision on deposits is made conditional on
Ω0,t which excludes the time period t shocks from the time t information set. Since
households cannot immediately adjust their nominal savings, a monetary shock
disproportionately affects banks reserves and, hence, the supply of loanable funds.
This creates the liquidity effect. Formally, we can proceed as in Fuerst (1992) and
write condition (2.34) as follows
Λt≡(l + ⅛)⅛ [⅛≡}
I Pt+ι J
Uct
pt
and
(2.36)
‰ {At} = O
Fuerst (1992) refers to Λt as the liquidity effect. One can think of it is as the
difference, at date t, between the value of money in the goods market and its value
in the loan market. When Λt < O, money is more valuable in the goods market
since households will be willing to borrow at a higher rate than if they had the
opportunity to do so. In this case, the loan market is relatively liquid. The variable
Λt would be zero if the households could choose the portfolios contemporaneously,
as in the standard Cash-In-Advance model.14 However, here it is zero only in
14This condition is (1 + Rt) = βEt {⅞7^7~vyy} fr°m where the Fisher Effect can be
deduced.