Evidence on the Determinants of Foreign Direct Investment: The Case of Three European Regions

3 Potential FDI determinants: some theory and descriptive statistics

The descriptive statistics on our three European regions show that most of the FDI inflows
originate from countries belonging to the European Union (Table 3). Therefore, it is reasonable to
consider that these FDI inflows are horizontal FDI.

3.1 A Theoretical framework of analysis

According to Feenstra (2004) among others, horizontal FDI occurs if a firm chooses to
produce in different countries with each plant selling locally to a market. In general, such a type of
FDI requires that the revenues of producing and selling locally should offset the plant fixed costs.
Horizontal FDI allows economies on transport costs and benefits from local production costs.

Looking at the fundamental determinants, Markusen (2002) argues that there are two factors
that turn out to be crucial for the existence of horizontal FDI: the size of the local markets and the
marginal production cost in the case of producing directly in the host market. The first factor is
evident: firms invest abroad to serve the local host market. Therefore, the size of the local demand
(known also as market size or market potential) will be determinant for the firm’s investment decision.
The second factor, the level of local production costs, will determine whether the firm produces locally
to sell locally or whether it supplies the host market by exporting its home-based production.

Following Feenstra (2004) and Markusen (2002), we develop a simple standard theoretical
framework describing the determinants affecting the choice between exporting and investing
(horizontal FDI) in a host economy.

We consider such a decision process for a firm under monopolistic competition, i.e. the firm
can fix its selling price by applying a mark-up over the production costs. Let us concentrate on the
choice of exporting or investing in region j faced by a firm initially located in region i. The size of the
mark-up relies on the elasticity of the demand (σ>1) the consumers address to the firm’s supply. We
model the utility function of consumers in region j with a CES (constant elasticity of substitution)
function. If it exports from region i to region j, the firm incurs a transport cost equal to Tij. We assume
that the firm produces the output just by using labor input.

First, let us concentrate on the export option. When producing in region i and then exporting in
region j, the firm faces the demand of the local consumers for a variety of the good it produces (cij) at
prices pij (pij= Tij pi , namely the local price in region j is the level of prices in region i corrected by the
transport cost), as:

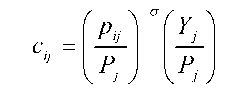
H Yj 'ʌ

(1)

where Yj is region j’s GDP and Pj refers to overall price index defined as:

Pj = r∑Ni(Pij)1

i=1

and where Nj is the number of goods imported by the region j.

The unique input is labor and the correspondent production function is Li=βyi with β, the
marginal cost and yi (=cij Tij ) the whole output for export. Each unit of labor is paid at wage wi. In the
export option, the total profits of exported quantities (for a firm) can be computed and are equal to
pi yi - wi Li. By replacing the proper expressions, we get the total profits for export:

<<   4   5   6   7   8   9   10   >>

More intriguing information