The fundamental determinants of financial integration in the European Union

Table 1 - The decomposition of the onshore covered nominal interest rate differential

(1) Offshore covered nominal interest rate differential
,            . Euro . * Euro , -t + к          ч

Фа™ = ≈,,>÷s “ ^l<,ι.l - </>    “S, )

(2) Domestic onshore-offshore closed nominal interest rate differential

.            _ .               . Euro

ɪ Domestic t, t + к ɪ t, t + к

(3) Foreign offshore-onshore closed nominal interest rate differential
.           _ ∙ * Furo _ ∙ ’

ɪ Foreign 11, t + к * t, t + к

(4)=(1)+(2)+(3) Onshore covered nominal interest rate differential
Φ Φ Domestic ⁺ $ foreign ⁺ Φ Euro

i,,,_tt - √,.→ - (f,'^t* -s,) =

[ "_f,.÷_l - ^l>,<÷tl ⁺ [≈<.<÷s-^,>.<÷tl ⁺ [ ≈<,>÷s - >>,<÷t - (∕>   -S,)]

Now, we may derive our measure for the intensity of capital controls. The domestic intensity of capital controls may be
approximated by the adjusted domestic covered nominal interest rate differential

Domestic Φ Φ Foreign Φ Domestic ⁺ Φ Euro ɪ t, t + к 4 ,t tk (ʃɪ $ ï )

while the foreign intensity of capital controls may be approximated by the adjusted foreign covered nominal interest rate differential

Foreign Φ Φ Domestic Φ Foreign ⁺ Φ Euro t, t + к ɪ t, t + к (ʃɪ ® Г

where banks ensure that offshore covered nominal interest rate parity holds continuously. That is, we may write

. Euro        . » Euro      _t rt + к         -.

>>,>÷t = ≈<,>÷s ⁺ <∕<   -s,)

and

. » Euro      . Euro        _t rt + к         -.

>>,,÷t = ≈<,>÷S - <∕<   -s,)

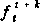
domestic onshore nominal rate of interest at time t on a k-period bond held between time t and t+k
domestic offshore nominal rate of interest at time t on a k-period bond held between time t and t+k
forward exchange rate at time t for the delivery of foreign currency at time t+k

spot exchange rate at time t (defined as units of domestic currency per unit of foreign currency)
holding period of the underlying debt instrument

denotes a foreign variable

Source: Goldsbrough and Teja (1991) and authors’ own summary of the literature.

Consequently, the domestic intensity of capital controls may either be measured by the domestic onshore-
offshore closed nominal interest rate differential

or by the adjusted domestic covered nominal interest rate differential

_ .          _ . * Euro _ f rt + k _

Domestic t , t + к t , t + к ∖J t         ^t

Capital controls will be an important reason for significant deviations from onshore covered nominal interest
parity.⁷ Since offshore covered nominal interest rate parity is zero by assumption, it follows that any
differential between the Euro-rate and the domestic rate on a comparable asset is likely to reflect domestic
capital controls. Closed and adjusted covered nominal interest rate differentials have been widely used to

⁷ More precisely, capital controls that are economically significant -- thus lying outside a small band of differentials created by
transaction costs.

<<   2   3   4   5   6   7   8   >>

More intriguing information