Testing for One-Factor Models versus Stochastic Volatility Models

propose to extend the different one-factor models by adding a stochastic volatility term, and suggest
models in which volatility depends on both the level of the underlying variable and a latent factor,
driven by a different Brownian motion.⁵

In particular, it should be stressed that in our procedure we compare generic classes of one
factor versus stochastic volatility models, without any functional form assumption on either the
drift or the variance term.

We state the hypothesis of interest as

H0 : σ_t² = σ² (Xt) , a.s.

versus the alternative

HA : σ_t² = g (ft) , a.s.

where ∀ω ∈ Ω⁺, ∣J0¹ (g (f_s) — g (Xs))ds| = 0 and Pr(Ω⁺) = 1, with Ω⁺ ∈ Ω, and Ω denotes the
probability space on which (ft ,Xt) are defined.

Thus, under the null hypothesis the volatility process is a measurable function of the return
process Xt . On the other hand, under the alternative, the volatility process is a measurable function
of a possibly unobservable process ft . In the paper, we simply require that the occupation densities
of the observable process Xt and of the (possibly) unobservable factor ft do not coincide. In fact, if
they do coincide, then the integrated volatility process would be almost surely the same under both
hypotheses. Finally, note that the case of σ_t² = σ² (Xt) g(ft) falls under the alternative hypothesis,
while the case of a constant variance falls under the null.

In the sequel, we assume that we have data recorded at two different frequencies, over a fixed
time span, which for sake of simplicity, but without loss of generality, is assumed equal to 1.⁶ More
specifically, we assume to have n and m observations, with m ≤ n, so that the discrete sampling
interval is equal respectively to 1/n and 1/m.

The proposed test statistics are based on

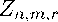
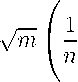
L^{( n-1}) ^rJ

Sn²(Xi/n) — RVm,r

where r ∈ (0, 1],

S 2 X X  ʌ _ Σ n=1 ¹ {l^xj∕n-Xi∕nl<ξn}n ( X^{( j + 1) /n} — ^Xj/n )

Sn ^{( x} i^/n )             ^ n-1

j=ι=ι¹ {∣Xj∕n-Xi∕n∣<ξn}

⁵Andersen and Lund (1997) find that the inclusion of a stochastic volatility component in a square root model
helps the elasticity parameter to fall in the stationary region. Durham (2003) finds that, although the addition of a
second factor increases the likelihood, it has very little impact as to what concerns bond pricing.

⁶ In Section 3, reporting the results of the simulation study, we will consider a time span equal to five days.

<<   3   4   5   6   7   8   9   >>

More intriguing information