rates in the euro area, and the rate on primary credit in the US; see, e.g., Hartmann et al.,
2001; and ECB, 2004), we assume that banks can borrow at a rate rIB and lend at a rate
rIL, independently of the counterparty. Our focus is on the amount of public liquidity the
banking system may need.
Given the presence of aggregate uncertainty, there may be an aggregate shortage or
an aggregate excess of private liquidity on the market. An aggregate shortage of private
liquidity occurs whenever banks’ aggregate demand for liquidity is higher than the aggre-
gate supply of private liquidity represented by the sum of individual banks’ reserves, i.e.,
whenever
NN
xi > Ri.
(5)
Denoting as Xi = PiN=1 xi = PiN=1 δiDi banks’ aggregate demand for liquidity with density
function f(Xi), we express the probability with which an aggregate shortage of private
liquidity occurs through the aggregate (or systemic) liquidity risk as
Φ = prob
N
Xi>
i=1
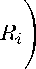
Di
= f(Xi)dXi,
Ri
(6)
and its expected size through the expected aggregate (or systemic) liquidity needs as
Di
P Ri
N
Xi - Ri f(Xi)dXi.
i=1
(7)
The aggregate liquidity risk (6) and the expected aggregate liquidity needs (7) can then be
interpreted as measures of the degree to which the banking system depends on the public
supply of liquidity, in the spirit of Holmstrom and Tirole (1988). Formulated differently, they
are indicators of the frequency and the size of central bank operations in the implementation
of monetary policy, and more generally of the attentiveness that the central bank has to
exert to implement monetary policy and ensure the stability of the interbank market.
The timing of the model is summarized in Figure 2. At date 0 banks compete in prices on the
loan market, choose reserve holdings, and raise deposits. After liquidity shocks materialize
at date 1, the interbank market opens. At date 2 loans mature, and remaining claims from
deposits and the interbank market are settled.
10
More intriguing information
1. The name is absent2. The Employment Impact of Differences in Dmand and Production
3. Importing Feminist Criticism
4. A Regional Core, Adjacent, Periphery Model for National Economic Geography Analysis
5. Subduing High Inflation in Romania. How to Better Monetary and Exchange Rate Mechanisms?
6. The name is absent
7. The name is absent
8. The name is absent
9. Political Rents, Promotion Incentives, and Support for a Non-Democratic Regime
10. Target Acquisition in Multiscale Electronic Worlds