Nonparametric cointegration analysis

times n², converge jointly in distribution to the ordered solutions of the generalized

eigenvalue problem ^det[ W,m ^{λ λ}Vs;q r,m] = ^0, where   Ws,m ^ς ∑ Z1Y 2^Y”^Y” T^,

(

∑γ 2y.“y;

^vk1

(

m

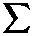
I^{b 1}

Y
m

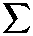
k= 1

m

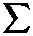
I^k=1

[cf. (23)], and the Y_k^** and X^*_k involved are independent s-variate and q-r-variate, respectively,
standard normal random vectors.

Note that the matrix V_s^*_{, q-r,m} in (32) differs from the matrix V_s^*_,m defined by (23) with r
replaced by s in that in the latter case the vectors X^*_k are (q-s) × 1 rather than (q-r) × 1.

If the null hypothesis (29) is false, then the matrix H can be written as

Then again it follows straightforwardly from (15), (17) and (30) that

D            ^m

H A. H →T^τ_lRq^lτrC(1)∑ X_lXk^τC(1)^τR_rrΓ,

k= 1

and

19

<<   16   17   18   19   20   21   22   >>

More intriguing information