Nonparametric cointegration analysis

JxFk(x)dx о 0, ⁽²⁸⁾

respectively, and to verify afterwards that the optimal weight functions F_k satisfy the stronger
conditions (6) and (7).

Without loss of generality we may represent the functions F_k by their Fourier flexible
form

∞∞

Fk⁽^x) ^α^αo,k ⁺ ∑ ^αj,k^cos(2^j^π^x) ⁺ ∑ ^β_j,k^sin(2^j^π^x)

Then by some tedious but straightforward calculations it can be shown that:

Lemma 6. The conditions (27), (28), (8), (9), and (10) now read as:

Fk⁽^χ)d^χ^{α α}ok - ⁰

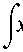
;(χ)dχ - -F-∑ ^β²^π J=1 J

ffF_k(x )Fm (y )min(x, y ) dxdy

8π²

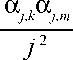
÷Σ

J=1

^βJ,k^βJ,

0 if k ≠ m ,

∞

F⁽^x ) [Fm (y ) dyd^x = -_r- Σ
^{4 4 4}^П 7=1

J, k^t^J, m

V^j-¹

∞

j=1

J,m J,k

^[^Fk⁽^x )Fm ⁽^x ) ^{dx =} ʌ

∞

V α..α.

X-7 j, k j,

Ij'¹

-∞

÷ βjkβ rn_t

0 if k ≠ m .

Combining (1) and the results of Lemma 6, we have