Nonparametric cointegration analysis

in which it is applied is more natural than for a trace test.

4.2. The choice of "m"

The limiting distribution of the lambda-min test under the null as well as under the
alternative depends on the test parameter m, and so does the α×100% critical values K_α,q-r,m,
say, as well as the power function. These critical values, which are presented in the separate
appendix to this paper for q-r = 1,..,5 and m = q-r,...,20, with the weight functions F_k
chosen as in Lemma 3, are calculated on the basis of 10,000 replications of the generalized
eigenvalue problem (20). These critical values increase with m. Now the power of the test
against the alternative H_r+1 is

≤n

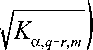
P(^λ_rr,m ≤ Kα,_rr,m) ≈ P ^λ1m

where, by Chebishev’s inequality, the latter probability is bounded from below as follows:

Lemma 5.

× traceRjTiD(1)D(1)TR,J
n

This result suggests to choose m such that the right hand side of (25) is maximal, subject to
the condition m ≥ q. The values of m involved are presented in Table 1, for the case where
the weight function F_k are chosen as in Lemma 3 (for which γ_k =2πk), and the
corresponding critical values are presented in Table 2.

<Insert Tables 1-2 about here>

14

<<   11   12   13   14   15   16   17   >>

More intriguing information