Nonparametric cointegration analysis

Note that Assumption 2 guarantees that the matrix V_r,m is a.s. nonsingular.
Denoting

Xk - RRTkc(1)C(1)TR J'⁴RqT,C(1)Xk, Yk = RTC(1)C(1)^tX_j,J'÷Rr(1) Y,,
and using the result of Andersen, Brons and Jensen (1983), it follows straightforwardly from

Lemma 4:

Theorem 1. Let λ₁ ,_m ≥ .. ≥ λ_q,_m be the ordered solutions of the generalized eigenvalue problem

defA λ λ(B +n ²A ¹)1 = 0,
|_ m mm          m ⁷J ’

and let λ_1,m ≥ ... ≥ λ_q-r,m be the ordered solution of the generalized eigenvalue problem

m

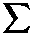
v^k1

(20)

where the X^*_i ’s and Y^*_j ’s are i.i.d. N_q-r(0,I_q-r). Ifz_t is cointegrated with r linear independent
cointegrating vectors then under Assumptions 1-3, (λ₁ ,_m ,..,λ_q,_m ) converges in distribution to
(λ1,m,...,λq-r,m,0,..,0).

In order to show how fast (λ_q-r+1 ,_m ,..,λ_q,_m ) converges to (0,....,0), observe from Lemma
4 that

O

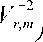
Moreover, it is easy to see that the solutions μ_j,_m of the generalized eigenvalue problem
ⁱ +n-2A^-1)R∣R^taR'ɪ -μI

m             m ⁷ / ∖ n * T T

11

<<   8   9   10   11   12   13   14   >>

More intriguing information