are just the reciprocals of n2λj,m. Thus again referring to Andersen, Brons and Jensen (1983) it
follows that n2(λq-r+1 ,m, .. , λq,m ) converges in distribution to the ordered eigenvalues of the
matrix Vr,m2 . Finally, observe that, with X*k defined by (18) and
Y" R {RTτD(1)D(1)trJ'÷R,τD(1)Yt (- Nr[0,Ir]), (21)
we can write the matrix Vr,m as
(22)
Vr,n, - D(1)D(1) R’ Vr'mi' D(1)D(1) τRr)4
where
V,
r,m
∑ γ 2 yΓyΓ
k- 1
(23)
Y YY
Λ,
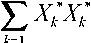
Thus we have:
Theorem 2. Under the conditions of Theorem 1, n2(λq-r+1,m, .. , λq,m) converges in distribution
to (λ*1,m2,...,λ*r,m2), where λ*1,m ≥ ... ≥ λ*r,m are the ordered solutions of the generalized eigenvalue
problem
det V,m - λ RirτD(1)D(1)τRr) "
where the matrix Vr*, m is defined in (23) with the X*i ’s and Y*j*’s independent q-r-variate and
r-variate, respectively, standard normally distributed random vectors.
4. Testing the number of cointegrating vectors
12
More intriguing information
1. Spectral calibration of exponential Lévy Models [1]2. The Works of the Right Honourable Edmund Burke
3. The name is absent
4. The name is absent
5. The name is absent
6. National urban policy responses in the European Union: Towards a European urban policy?
7. Wage mobility, Job mobility and Spatial mobility in the Portuguese economy
8. Keynesian Dynamics and the Wage-Price Spiral:Estimating a Baseline Disequilibrium Approach
9. On Evolution of God-Seeking Mind
10. Activation of s28-dependent transcription in Escherichia coli by the cyclic AMP receptor protein requires an unusual promoter organization