Assessing Economic Complexity with Input-Output Based Measures

and define the Sectoral Average Propagation Lengths (APLs, which we can represent on
a nxn matrix; let us call it the APL matrix ):

h

APL_ii = -^l, for : i ≠ j
ij l

ij

These values are the base of the M10 - APLU: Average Propagation Lengths

(Unweighted) measure:

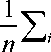
¹ ∑ jAPL =¹ ∑ j ¹ ∑A^pL_t
n ^j           n ^j n ^t

Another recent measure, explicitly made for quantifying economic complexity as input-
output interdependence, is proposed by Amaral et al. (2007), based on Amaral (1999).

This measure considers i) a “network” effect, which gives the extent of the direct and
indirect connections of each part of the system with the other parts, and where more
connections corresponds to more complexity; and ii) a “dependency” effect, i.e. how much of
the behavior of each part of the system is determined by internal connections between the
elements of that part - which means more autonomy and less dependency - and how much of
that behavior is determined by external relations, i.e. relations with other parts of the system
- which means less autonomy and greater dependency.

<<   7   8   9   10   11   12   13   >>

More intriguing information