The cash outflow postponement component assumes the same value at t0, t1 and at t2
while it is zero at t3 (at expiry the cash outflow cannot be postponed any longer). Moreover
it is independent from the project value. The reversibility component decreases with time
and at any date tn it is a monotonic decreasing function of the value of the project.
Conversely the opportunity cost (lost payout component) is independent of time, whereas it
linearly increases with the value of the project.
A simple argument establishes that at any tn the optimal stopping policy can be
expressed in the following terms: exercise if Stn>S*tn; do not exercise otherwise. The
optimal stopping rules reflects the intuition that when the stock price is sufficiently high the
probability of incurring losses at expiry is quite low (low protection) while the lost payout
due to because of waiting becomes significant (high opportunity cost).
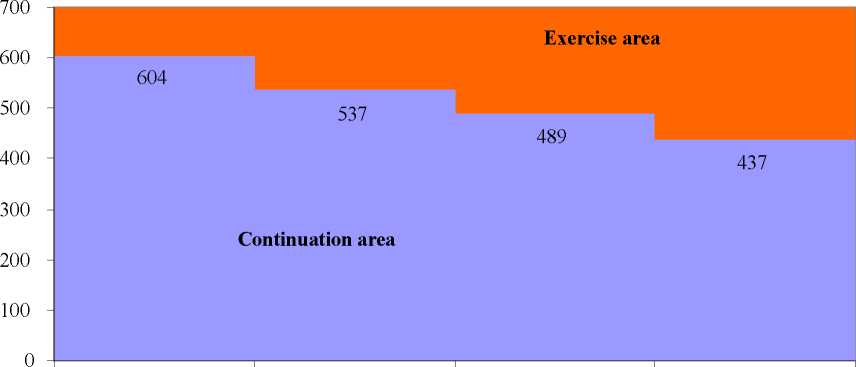
Since the value of protection falls with time, the critical values S*tn, above which it is
optimal to carry out the project, decreases as the date of expiry becomes closer (see Figure
7).
Figure 7 -Critical values S*t0, S*t1, S*t2 and S*t3
t0 t1 t2 t3
18
More intriguing information
1. The name is absent2. New urban settlements in Belarus: some trends and changes
3. Permanent and Transitory Policy Shocks in an Empirical Macro Model with Asymmetric Information
4. Review of “From Political Economy to Economics: Method, the Social and Historical Evolution of Economic Theory”
5. The Clustering of Financial Services in London*
6. The name is absent
7. An Attempt to 2
8. Accurate, fast and stable denoising source separation algorithms
9. Olfactory Neuroblastoma: Diagnostic Difficulty
10. The name is absent