Multifunctionality of Agriculture: An Inquiry Into the Complementarity Between Landscape Preservation and Food Security

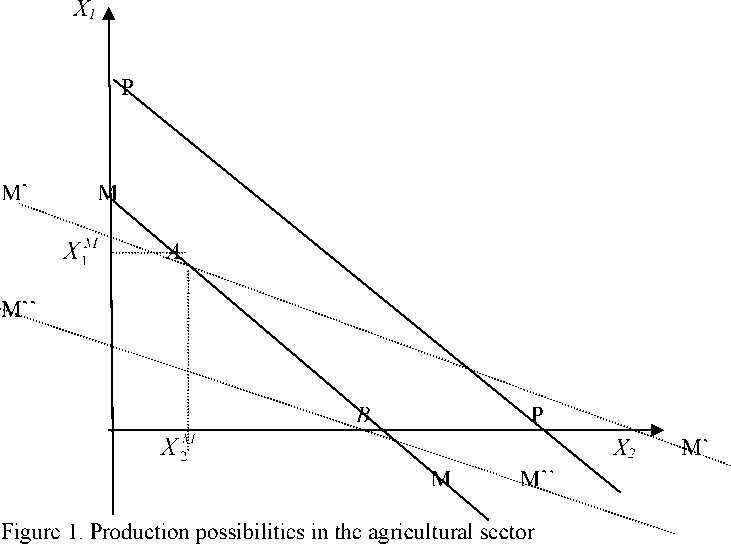
In figure 1 we have drawn the production possibility frontier PP. The slope of PP equals -γ 2 ∕γ₁ .

Suppose that the crisis menu is given by X^M = (X₁^M , X₂^M ) marked as A in the figure. The
land requirement for producing X ^M is denoted L^M , and the production possibility frontier given this
land requirement is the solid line MM.

Assume that we choose a level of land use that is not sufficient to guarantee complete food
security, thus we are only able to produce a share, λ, of the crisis menu. Define X=(X1,X2)= λX^M . For
the moment we abstract from stockpiling and aid, and imports of the two commodities, μ_i, is treated as
uncertain. (1) can then be written as:

Pr(X+μ≥XM) ≥π;      μ≥0,

where μ=(μ₁, μ₂). Pr(λXM+μ≥XM)< 1 for λ<1, and the probability is 1 when λ≥ 1.

The point of departure for Gulbrandsen and Lindbeck is an inefficient agricultural sector. This
means that the net cost per hectare land, NCHi, is positive:

for both commodities. Without support nothing will be produced. Food security is an argument for
agricultural support, i.e. land must be available when a crisis arises.

Assume that it is more costly (per hectare) to produce X1 than X2, so NCH2<NCH1, and assume
that we require complete food security (λ=1).

<<   1   2   3   4   5   6   7   >>

More intriguing information