10
stringency of the QAS to implement and the output rate are usually interrelated, specifically
through the cost function. The processor’s problem is
,z,l, w π( y, s ; a )
max E (∏( y, s )) = max----—-——
y≥0,s∈S y≥0,s∈S1- βm ( s,ω)
and the corresponding first-order conditions are given by
(3)
dE (∏( y, s )) _ ∂π( y, s ; a ) ≤ 0
∂y ∂y
y≥0
(4)
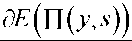
∂s
∂π( y, s ; a )
∂s
+ π( y, s ; a )
β ∂m ( s, ω )
-----∂s—TV ≤ 0, s ≥ 0.
The Hessian for this problem (which needs to be negative semidefinite for a maximum)
is the 2x2 matrix in system (5) below. Equations (3) and (4) have the usual interpretation.
Equation (3) is the standard necessary condition for the monopolist profit-maximization
problem and will not be discussed further. Equation (4) states that the level of stringency
should be increased until the marginal benefits of increased stringency equal the marginal
costs. Marginal benefits of an increase in s equal the change in the proportion of purchases that
are of high quality multiplied by the probability that low-quality output will be discovered,5
the per-period profit rate, and a factor that takes into account the multi-period nature of the
problem at hand. The marginal benefits of increased assurance rise as the quality of the good is
more readily observable by the processor’s customers and as the potential punishments for
false certification become more severe. Switching to the second state of the world is a harsher
punishment when per-period profits are high and when the future is important to the processor.
The marginal cost of an increase in s is simply the increase in costs that must be incurred to
implement a more stringent QAS. The first-order conditions can in principle be solved to
More intriguing information
1. Restricted Export Flexibility and Risk Management with Options and Futures2. The name is absent
3. The name is absent
4. Herman Melville and the Problem of Evil
5. THE CO-EVOLUTION OF MATTER AND CONSCIOUSNESS1
6. Strategic monetary policy in a monetary union with non-atomistic wage setters
7. A Note on Productivity Change in European Co-operative Banks: The Luenberger Indicator Approach
8. Gerontocracy in Motion? – European Cross-Country Evidence on the Labor Market Consequences of Population Ageing
9. The urban sprawl dynamics: does a neural network understand the spatial logic better than a cellular automata?
10. Exchange Rate Uncertainty and Trade Growth - A Comparison of Linear and Nonlinear (Forecasting) Models