Reputations, Market Structure, and the Choice of Quality Assurance Systems in the Food Industry

21

current state is i . Note that any state can follow state 1, but neither state 1 nor state 3 can be
reached after state 2. In the jargon of Markov chains, state 4 is absorbing, that is, once it is
reached, the system stays in it forever, or, alternatively, it will go to other states with
probability zero. Note that as required in a Markov matrix, all the entries are nonnegative and
∑^j_j⁼₌₁⁴Mi,j=1 for i =1,...,4.¹⁰

With this in place and noting that processor 1 makes zero profits in states 3 and 4, we

can write the firm’s first-stage problem as
where k = 1,2, π_k¹ , denotes per period profits for processor 1 when there are k market
participants; e_k is a 4x1 vector that has zeros everywhere except for a 1 in the kth position;

max E ∏¹ = max <

∙¾∈ 5             ⅛∈ 5

∞

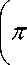
(s₁,s₂)∑βⁱe₁Mⁱe₁^T
i=0

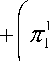
(s₁,s₂

∞

)∑β^je2M^je2^T

j=1

and T is the transpose operator.

Equation (10) specifies that processors maximize the profits in the duopoly and
monopoly situation, weighted by the likelihood of the different scenarios, which they can
affect by the stringency of the QAS they choose. The first-order condition for this problem is
(11) ∏∑βeM∙e1 + ∏ ∑β-e 'M e + ^d-∏∑ jM>e∖ + ∏∑βe_: ^?M^e\ ≤0,
∂s1i=0i=0∂s1∂s1j=1j=1∂s1

with equality if s₁ > 0 . Of course, a symmetric equation exists for the other processor.

Equation (11) has the usual interpretation. Processors will equate marginal benefits
(given by the second and fourth terms in (11)) against marginal costs (given by the first and
third terms in (11)) in their choice of QAS. The new terms are associated with the introduction
of the possibility of being a monopolist if firm 2 loses its reputation first. An equilibrium for

<<   18   19   20   21   22   23   24   >>

More intriguing information